Vector Cross Product Calculator

All About Vector Cross Product Calculator

When two directions meet in space, they don’t always align. Sometimes, they create something new, a vector that rises at a right angle to both. That’s the idea behind the vector cross product. It’s not just about combining motion; it’s about finding direction, orientation, and depth. You’ll see it in torque from a wrench, the spin of a wheel, or the path of a charged particle in a magnetic field.

This article will guide you through what the cross product is, how to calculate it, where it appears in real life, and how to explore it using Symbolab’s Vector Cross Product Calculator.

What Is the Vector Cross Product?

The vector cross product takes two vectors in three-dimensional space and produces a third vector that is perpendicular to both. This new vector shows not just a result, but a direction — one that points outward from the plane formed by the original two.

Unlike the dot product, which tells you how much two vectors align, the cross product tells you how they interact to create rotation or orientation. It’s used when direction matters: in torque, force, and geometry that lives in space, not just on a line.

The cross product is written as:

$\vec{a} \times \vec{b}$

And its result:

• Is a vector
• Has a magnitude equal to the area of the parallelogram spanned by $\vec{a}$ and $\vec{b}$. If one or both vectors carry physical units, say metres and newtons, the magnitude still equals $|\vec{a}\times\vec{b}| = |\vec{a}||\vec{b}|\sin(\theta)$, but the “area” now inherits those units, e.g. $\text{N}\cdot\text{m}$ for torque.
• Points in the direction given by the right-hand rule

In real-world terms, think of turning a screwdriver, swinging a door, or watching how one motion causes another to twist out of plane. The cross product captures that.

Understanding What the Vector Cross Product Contains

The cross product always happens between two vectors in three-dimensional space. It creates a new vector with two key features:

• Direction: perpendicular to both original vectors
• Magnitude: equal to the area of the parallelogram they span

So every cross product result can be understood in terms of:

• Its x, y, and z components — the actual values in the resulting vector
• Its orientation — which direction it points in space, guided by the right-hand rule
• Its size — how large the area is, given by the formula: $|\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin(\theta)$ where $\theta$ is the angle between the vectors

There aren’t multiple types of cross product, but the result shifts depending on:

• The angle between the vectors
• Whether the vectors lie in the same plane or are parallel (if they are, the cross product is the zero vector)
• The units you’re working with-force, motion, or position

The cross product behaves consistently, but it takes different roles depending on the problem. In physics, it might describe rotational force. In 3D modeling, it defines surface normals. In each case, the mechanics are the same, but the meaning shifts.

Geometric Meaning and the Right-Hand Rule

The vector cross product creates more than a number. It gives you a new vector that is perpendicular to both of the original ones. That direction is not a guess or a coincidence. It comes straight from geometry.

Imagine two arrows lying flat, one pointing north, the other pointing east. The cross product of those two arrows points straight up, out of the plane they form. It builds a third direction that lifts off the page.

To figure out which way the result points, you can use the right-hand rule.

Here’s how:

• Point your index finger in the direction of the first vector
• Point your middle finger in the direction of the second
• Your thumb will then point in the direction of the cross product

If you switch the order of the vectors, your thumb flips. That’s why $\vec{a} \times \vec{b}$ and $\vec{b} \times \vec{a}$ point in opposite directions. The cross product depends on order.

This result also has a size. The length of the new vector equals the area of the parallelogram formed by the original two. So you’re not just getting direction — you’re getting a measure of how much space the vectors span. Whenever two vectors act together in space, the cross product shows you how that interaction twists, turns, or lifts into something new.

Mathematicians can define cross-product-like operations outside 3-D—there’s a special 7-D version and a general “wedge product” that works in any dimension. For everyday physics and engineering, we stay in 3-D, but curious readers might enjoy looking those up!

Real-Life Applications of Vector Cross Products

The cross product comes to life anywhere force meets rotation, or direction leads to motion. It might sound like something out of physics class, but it quietly powers much of the world around us.

• Torque and tools: Twist a wrench. The way you apply force, and the direction of that force, determine how effectively the bolt turns. The cross product describes that rotation. The longer the wrench and the more perpendicular your push, the more torque you create.
• Rotating wheels and levers: On a bicycle pedal, your foot pushes down at an angle while the crank rotates. The cross product captures that interaction — it tells you how much turning force your pedaling actually produces.
• Magnetic force on a moving charge: In physics, when a charged particle moves through a magnetic field, the force it feels is not in the same direction as either the motion or the field. Instead, it comes out at a right angle to both. That direction and strength are found using the cross product.
• Airplane stability and lift: In aerodynamics, cross products help describe how changes in airflow direction affect lift, torque, or roll. Vectors aren’t just distances — they define how a plane tilts, turns, or holds steady in the sky.
• 3D modeling and surface orientation: In animation, engineering, or computer graphics, every surface has a “facing” direction — a normal vector. That direction is often calculated using the cross product of two edges of a triangle. It helps determine how light hits a surface, or how two objects fit together in space.

The cross product isn’t a rare operation. It shows up every time vectors meet at angles, and something turns or shifts as a result. Wherever movement and space interact, the math behind it often comes from here.

How to Calculate the Cross Product Manually

To calculate the cross product by hand, you use something that might feel a bit unexpected at first — a determinant from matrix math.

$(1, 2, 3)×(1, 5, 7)$

Step 1: Set up a $3 \times 3$ matrix

• The first row holds the unit vectors: $\hat{i}$, $\hat{j}$, and $\hat{k}$
• The second row is the first vector: $(1,\ 2,\ 3)$
• The third row is the second vector: $(1,\ 5,\ 7)$

​​

Step 2: Expand the determinant

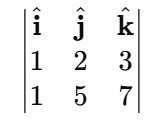
We take the determinant across the top row:

$\vec{a} \times \vec{b} = \hat{i}(2 \cdot 7 - 3 \cdot 5) - \hat{j}(1 \cdot 7 - 3 \cdot 1) + \hat{k}(1 \cdot 5 - 2 \cdot 1)$

$= \hat{i}(14 - 15) - \hat{j}(7 - 3) + \hat{k}(5 - 2)$

$= \hat{i}(-1) - \hat{j}(4) + \hat{k}(3)$

$= -\hat{i} - 4\hat{j} + 3\hat{k}$

Final Result: $\vec{a} \times \vec{b} = (-1, -4, 3)$

This is your cross product, a new vector that is perpendicular to both original vectors. It carries both direction and magnitude, describing how these two vectors act in space when combined.

Common Mistakes to Avoid

Cross products follow a clear path, but it’s easy to miss a turn if you're not paying attention. These are the most common missteps students run into, and a few ways to catch them early.

• Mixing up the order of vectors: The cross product is not commutative. $\vec{a} \times \vec{b} \ne \vec{b} \times \vec{a}$ In fact, $\vec{b} \times \vec{a} = -(\vec{a} \times \vec{b})$ Reversing the order flips the direction of the result.
• Using dot product logic by accident: Sometimes students confuse cross product with dot product. Remember:
  • The dot product gives a scalar (a number)
  • The cross product gives a vector
  • Look at your result. If it’s a single value instead of a vector like $(-1,\ -4,\ 3)$, you're in the wrong operation.
• Forgetting to apply the determinant properly: It’s tempting to skip the structure, especially under time pressure. But writing out the full $3 \times 3$ matrix helps keep signs and positions straight.
• Dropping negative signs: The signs that appear during determinant expansion matter. Losing a minus sign early can quietly distort your entire result. Slow down during that step and check each calculation.
• Using two-dimensional vectors: The cross product only applies to vectors in three dimensions. If your vectors have only two components, you’re either working in 2D or you need to treat the third component as 0.

Mistakes are part of the process, but so is catching them. Cross products reward careful setup and steady hands. A few extra seconds of structure can save you from minutes of rework.

How to Use Symbolab’s Vector Cross Product Calculator

When you're working with vector cross products, Symbolab helps you see each part of the process. It's not just an answer tool. It’s a way to learn by doing.Here’s how to use it:

Step 1: Enter the expression

• Type it directly using your keyboard or use the math keyboard.
• Upload a photo of a handwritten expression or textbook with your camera.
• Use the Chrome extension to screenshot from a webpage.
• Try out the built-in example for practice

Step 2: Click “Go”

Step 3: Explore step-by-step solution

• You will see a full step-by-step breakdown, or you can choose to go through one step at a time, so nothing gets rushed.
• You can click on ‘Chat with Symbo’ about any part of the solution, and get guidance as you go.

Conclusion

The vector cross product builds something new from two directions, a result with both shape and strength. Whether you’re solving by hand or exploring with Symbolab, you’re learning how motion and geometry work together in space. That’s not just calculation. It’s insight. And it stays with you.