Read: Write the Equation of a Linear Function Part II
Learning Objectives
- Given a graph, write the equation of a linear function
- Given two function values and corresponding inputs, write the equation of the linear function passing through them
Now that we have written equations for linear functions in both the slope-intercept form and the point-slope form, we can choose which method to use based on the information we are given. That information may be provided in the form of a graph, a point and a slope, two points, and so on. Look at the graph of the function f below.
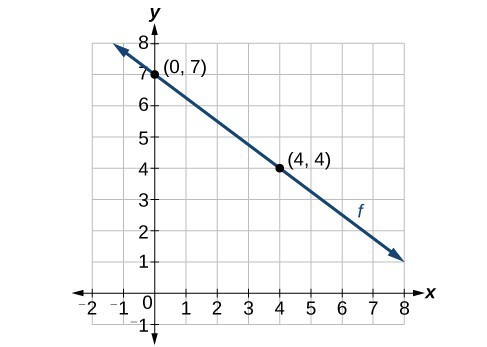 The function f passing through the points (0.7) and (4,4) with a negative slope.
The function f passing through the points (0.7) and (4,4) with a negative slope.We are not given the slope of the line, but we can choose any two points on the line to find the slope. Let’s choose [latex](0, 7)[/latex] and [latex](4, 4)[/latex]. We can use these points to calculate the slope.
Now we can substitute the slope and the coordinates of one of the points into the point-slope form.
If we want to rewrite the equation in the slope-intercept form, we would find
 Rewrite the equation in slope intercept form.
Rewrite the equation in slope intercept form.If we wanted to find the slope-intercept form without first writing the point-slope form, we could have recognized that the line crosses the y-axis when the output value is [latex]7[/latex]. Therefore, b = [latex]7[/latex]. We now have the initial value b and the slope m so we can substitute m and b into the slope-intercept form of a line.
So the function is [latex]f\left(x\right)=-\dfrac{3}{4}x+7[/latex], and the linear equation would be [latex]y=-\dfrac{3}{4}x+7[/latex].
Given the graph of a linear function, write an equation to represent the function.
- Identify two points on the line.
- Use the two points to calculate the slope.
- Determine where the line crosses the y-axis to identify the y-intercept by visual inspection.
- Substitute the slope and y-intercept into the slope-intercept form of a line equation.
Example
Write an equation for a linear function given a graph of f shown below.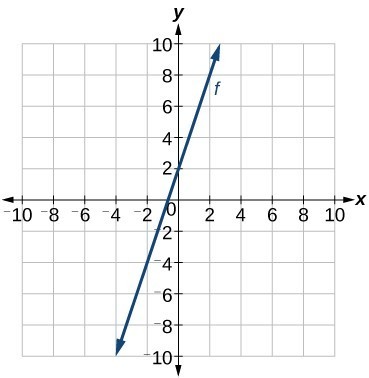
Answer:
Identify two points on the line, such as [latex](0, 2)[/latex] and [latex](–2, –4)[/latex]. Use the points to calculate the slope.
Substitute the slope and the coordinates of one of the points into the point-slope form.
We can use algebra to rewrite the equation in the slope-intercept form.
Analysis of the Solution
This makes sense because we can see from the graph below that the line crosses the y-axis at the point [latex](0, 2)[/latex], which is the y-intercept, so [latex]b = 2[/latex].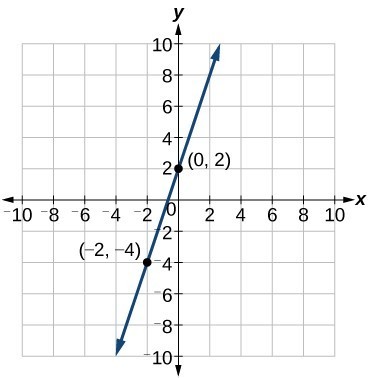 In the following video we show an example of how to write the equation of a line given it's graph.
https://youtu.be/mmWf_oLTNSQ
In the following video we show an example of how to write the equation of a line given it's graph.
https://youtu.be/mmWf_oLTNSQ
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 1: Find the Equation of a Line in Slope Intercept Form Given the Graph of a Line. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download free at : http://cnx.org/contents/[email protected]:1/Preface.
- Ex: Find the Linear Function Given Two Function Values in Function Notation. Authored by: for Lumen Learning. License: CC BY: Attribution.

Example
If f is a linear function, with [latex]f\left(3\right)=-2[/latex] , and [latex]f\left(8\right)=1[/latex], find an equation for the function in slope-intercept form.Answer:
We can write the given points using coordinates.
We can then use the points to calculate the slope.
Substitute the slope and the coordinates of one of the points into the point-slope form.
We can use algebra to rewrite the equation in the slope-intercept form.
Summary