Read: Solve Systems by Elimination
Learning Objectives
- Solve a system using the elimination method
- Solve a system using the elimination method when multiplication is required
- Recognize when a system is dependent using algebraic results
Example
Solve the given system of equations by elimination.Answer: Both equations are already set equal to a constant. Notice that the coefficient of [latex]x[/latex] in the second equation, [latex]–1[/latex], is the opposite of the coefficient of [latex]x[/latex] in the first equation, [latex]1[/latex]. We can add the two equations to eliminate [latex]x[/latex] without needing to multiply by a constant.
[latex]\begin{array}{l}3y=2\hfill \\ \text{ }y=\dfrac{2}{3}\hfill \end{array}[/latex]
Then, we substitute this value for [latex]y[/latex] into one of the original equations and solve for [latex]x[/latex][latex]\begin{array}{l}\text{ }-x+y=3\hfill \\ \text{ }-x+\dfrac{2}{3}=3\hfill \\ \text{ }-x=3-\dfrac{2}{3}\hfill \\ \text{ }-x=\dfrac{7}{3}\hfill \\ \text{ }x=-\dfrac{7}{3}\hfill \end{array}[/latex]
The solution to this system is [latex]\left(-\dfrac{7}{3},\dfrac{2}{3}\right)[/latex]. Check the solution in the first equation.[latex]\begin{array}{llll}\text{ }x+2y=-1\hfill & \hfill & \hfill & \hfill \\ \text{ }\left(-\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right)=\hfill & \hfill & \hfill & \hfill \\ \text{ }-\dfrac{7}{3}+\dfrac{4}{3}=\hfill & \hfill & \hfill & \hfill \\ \text{ }-\dfrac{3}{3}=\hfill & \hfill & \hfill & \hfill \\ \text{ }-1=-1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex]
We gain an important perspective on systems of equations by looking at the graphical representation. In the graph below, you will see that the equations intersect at the solution. We do not need to ask whether there may be a second solution because observing the graph confirms that the system has exactly one solution.
Example
Solve the given system of equations by the elimination method.[latex]\begin{array}{l}3x+5y=-11\hfill \\ \hfill \\ x - 2y=11\hfill \end{array}[/latex]
Answer: Adding these equations as presented will not eliminate a variable. However, we see that the first equation has [latex]3x[/latex] in it and the second equation has [latex]x[/latex]. So if we multiply the second equation by [latex]-3,\text{}[/latex] the x-terms will add to zero.
[latex]\begin{array}\ \hfill 3x+5y=−11 \\ \hfill −3x+6y=−33 \\ \text{_____________} \\ \hfill 11y=−44 \\ \hfill y=−4 \end{array}[/latex]
For the last step, we substitute [latex]y=-4[/latex] into one of the original equations and solve for [latex]x[/latex].[latex]\begin{array}{c}3x+5y=-11\\ 3x+5\left(-4\right)=-11\\ 3x - 20=-11\\ 3x=9\\ x=3\end{array}[/latex]
Our solution is the ordered pair [latex]\left(3,-4\right)[/latex]. Check the solution in the original second equation.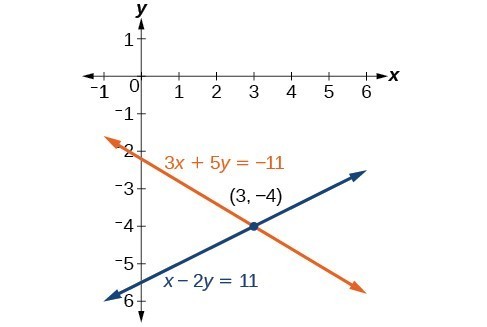
Example
Solve the given system of equations in two variables by elimination.Answer: One equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. The least common multiple is [latex]10x[/latex] so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate [latex]x[/latex] by multiplying the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex].
[latex]\begin{array}\ −10x−15y=80 \\ 10x−20y=60 \\ \text{______________} \\ \text{ }−35y=140 \\ y=−4 \end{array}[/latex]
Substitute [latex]y=-4[/latex] into the original first equation.[latex]\begin{array}{c}2x+3\left(-4\right)=-16\\ 2x - 12=-16\\ 2x=-4\\ x=-2\end{array}[/latex]
The solution is [latex]\left(-2,-4\right)[/latex]. Check it in the other equation.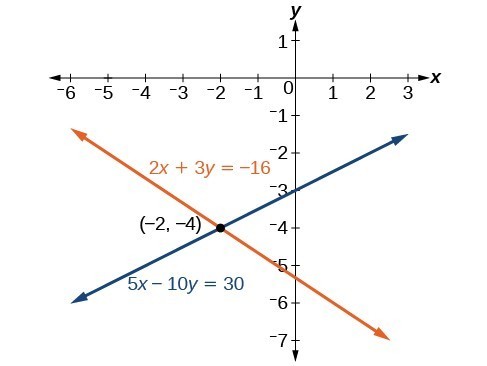
How To: Given a system of equations, solve using the elimination method.
- Write both equations with x- and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
Example
Solve the given system of equations in two variables by elimination.[latex]\begin{array}{l}\dfrac{x}{3}+\dfrac{y}{6}=3\hfill \\ \dfrac{x}{2}-\dfrac{y}{4}=\text{ }1\hfill \end{array}[/latex]
Answer: First clear each equation of fractions by multiplying both sides of the equation by the least common denominator
[latex]\begin{array}{l}6\left(\dfrac{x}{3}+\dfrac{y}{6}\right)=6\left(3\right)\hfill \\ \text{ }2x+y=18\hfill \\ 4\left(\dfrac{x}{2}-\dfrac{y}{4}\right)=4\left(1\right)\hfill \\ \text{ }2x-y=4\hfill \end{array}[/latex]
Now multiply the second equation by [latex]-1[/latex] so that we can eliminate the x-variable.[latex]\begin{array}{l}-1\left(2x-y\right)=-1\left(4\right)\hfill \\ \text{ }-2x+y=-4\hfill \end{array}[/latex]
Add the two equations to eliminate the x-variable and solve the resulting equation.[latex]\begin{array}\ \hfill 2x+y=18 \\ \hfill−2x+y=−4 \\ \text{_____________} \\ \hfill 2y=14 \\ \hfill y=7 \end{array}[/latex]
Substitute [latex]y=7[/latex] into the first equation.[latex]\begin{array}{l}2x+\left(7\right)=18\hfill \\ \text{ }2x=11\hfill \\ \text{ }x=\dfrac{11}{2}\hfill \\ \text{ }=7.5\hfill \end{array}[/latex]
The solution is [latex]\left(\dfrac{11}{2},7.5\right)[/latex]. Check it in the other equation.[latex]\begin{array}{c}\dfrac{x}{2}-\dfrac{y}{4}=1\\ \dfrac{\dfrac{11}{2}}{2}-\dfrac{7}{4}=1\\ \dfrac{11}{4}-\dfrac{7}{4}=1\\ \dfrac{4}{4}=1\end{array}[/latex]
Example
Find a solution to the system of equations using the elimination method.[latex]\begin{array}{c}x+3y=2\\ 3x+9y=6\end{array}[/latex]
Answer: With the elimination method, we want to eliminate one of the variables by adding the equations. In this case, let’s focus on eliminating [latex]x[/latex]. If we multiply both sides of the first equation by [latex]-3[/latex], then we will be able to eliminate the [latex]x[/latex] -variable.
[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \left(-3\right)\left(x+3y\right)=\left(-3\right)\left(2\right)\hfill \\ \text{ }-3x - 9y=-6\hfill \end{array}[/latex]
Now add the equations.[latex]\begin{array} \hfill−3x−9y=−6 \\ \hfill+3x+9y=6 \\ \hfill \text{_____________} \\ \hfill 0=0 \end{array}[/latex]
We can see that there will be an infinite number of solutions that satisfy both equations. If we rewrote both equations in the slope-intercept form, we might know what the solution would look like before adding. Let’s look at what happens when we convert the system to slope-intercept form.[latex]\begin{array}{l}\text{ }x+3y=2\hfill \\ \text{ }3y=-x+2\hfill \\ \text{ }y=-\dfrac{1}{3}x+\dfrac{2}{3}\hfill \\ 3x+9y=6\hfill \\ \text{ }9y=-3x+6\hfill \\ \text{ }y=-\dfrac{3}{9}x+\dfrac{6}{9}\hfill \\ \text{ }y=-\dfrac{1}{3}x+\dfrac{2}{3}\hfill \end{array}[/latex]
See the graph below. Notice the results are the same. The general solution to the system is [latex]\left(x, -\dfrac{1}{3}x+\dfrac{2}{3}\right)[/latex].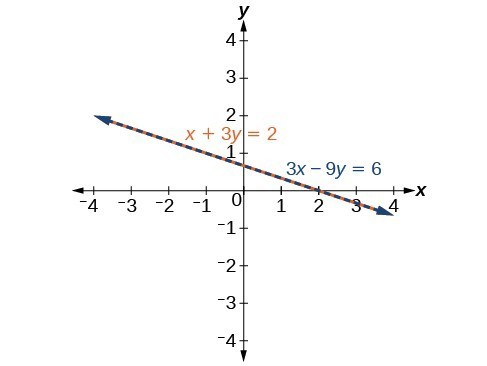
Licenses & Attributions
CC licensed content, Shared previously
- Ex 1: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 2: Solve a System of Equations Using the Elimination Method. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Eliminations (Fractions). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: System of Equations Using Elimination (Infinite Solutions). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: System of Equations Using Elimination (No Solution). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
