We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Graph Linear Functions

Learning Objectives

  • Graph linear functions using a table of values
  A helpful first step in graphing a function is to make a table of values. This is particularly useful when you don’t know the general shape the function will have. You probably already know that a linear function will be a straight line, but let’s make a table first to see how it can be helpful. When making a table, it’s a good idea to include negative values, positive values, and zero to ensure that you do have a linear function. Make a table of values for [latex]f(x)=3x+2[/latex]. Make a two-column table. Label the columns x and f(x).
x f(x)
Choose several values for x and put them as separate rows in the x column. These are YOUR CHOICE - there is no "right" or "wrong" values to pick, just go for it. Tip: It’s always good to include 0, positive values, and negative values, if you can.
x f(x)
[latex]−2[/latex]
[latex]−1[/latex]
[latex]0[/latex]
[latex]1[/latex]
[latex]3[/latex]
Evaluate the function for each value of x, and write the result in the f(x) column next to the x value you used. When [latex]x=0[/latex], [latex]f(0)=3(0)+2=2[/latex], [latex]f(1)=3(1)+2=5[/latex], [latex]f(−1)=3(−1)+2=−3+2=−1[/latex], and so on.
x f(x)
[latex]−2[/latex] [latex]−4[/latex]
[latex]−1[/latex] [latex]−1[/latex]
[latex]0[/latex] [latex]2[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]3[/latex] [latex]11[/latex]
(Note that your table of values may be different from someone else’s. You may each choose different numbers for x.) Now that you have a table of values, you can use them to help you draw both the shape and location of the function. Important: The graph of the function will show all possible values of x and the corresponding values of y. This is why the graph is a line and not just the dots that make up the points in our table. Graph [latex]f(x)=3x+2[/latex]. Using the table of values we created above you can think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid.
x f(x)
[latex]−2[/latex] [latex]−4[/latex]
[latex]−1[/latex] [latex]−1[/latex]
[latex]0[/latex] [latex]2[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]3[/latex] [latex]11[/latex]
Plot the points. The points negative 2, negative 4; the point negative 1, negative 1; the point 0, 2; the point 1, 5; the point 3, 11. Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge. A line through the points in the previous graph.   Let’s try another one. Before you look at the answer, try to make the table yourself and draw the graph on a piece of paper.

Example

Graph [latex]f(x)=−x+1[/latex].

Answer: Start with a table of values. You can choose different values for x, but once again, it’s helpful to include [latex]0[/latex], some positive values, and some negative values. If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid.

[latex]f(−2)=−(−2)+1=2+1=3\\f(−1)=−(−1)+1=1+1=2\\f(0)=−(0)+1=0+1=1\\f(1)=−(1)+1=−1+1=0\\f(2)=−(2)+1=−2+1=−1[/latex]

x f(x)
[latex]−2[/latex] [latex]3[/latex]
[latex]−1[/latex] [latex]2[/latex]
[latex]0[/latex] [latex]1[/latex]
[latex]1[/latex] [latex]0[/latex]
[latex]2[/latex] [latex]−1[/latex]
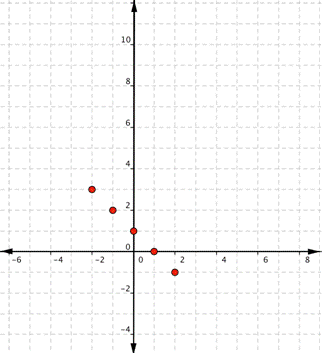
Plot the points. The point negative 2, 3; the point negative 1, 2; the point 0, 1; the point 1, 0; the point 2, negative 1.  

Answer

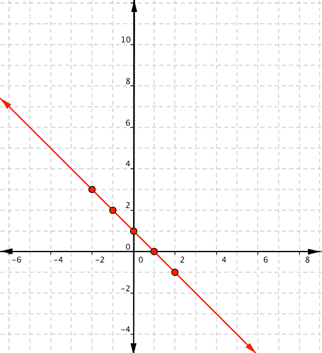Line through the points in the last graph. Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge.

In the following video we show another example of how to graph a linear function on a set of coordinate axes. https://youtu.be/sfzpdThXpA8 These graphs are representations of a linear function. Remember that a function is a correspondence between two variables, such as x and y.

A General Note: Linear Function

A linear function is a function whose graph is a line. Linear functions can be written in the slope-intercept form of a line [latex-display]f\left(x\right)=mx+b[/latex-display] where [latex]b[/latex] is the initial or starting value of the function (when input, [latex]x=0[/latex]), and [latex]m[/latex] is the constant rate of change, or slope of the function. The y-intercept is at [latex]\left(0,b\right)[/latex].

Licenses & Attributions

CC licensed content, Shared previously

  • Ex: Graph a Linear Function Using a Table of Values (Function Notation). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.