Read: Logarithmic Equations
Learning Objectives
- Use the definition of a logarithm to solve logarithmic equations
- Use a graph to verify or analyze the solution to a logarithmic equation
For example, consider the equation [latex]{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x:
Example
Solve [latex]2\mathrm{ln}x+3=7[/latex].Answer: [latex]\begin{array}{c}2\mathrm{ln}x+3=7\hfill & \hfill \\ \text{ }2\mathrm{ln}x=4\hfill & \text{Subtract 3}.\hfill \\ \text{ }\mathrm{ln}x=2\hfill & \text{Divide by 2}.\hfill \\ \text{ }x={e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{array}[/latex]
Analysis of the solution
The solution for the previous equation was [latex]x={e}^{2}[/latex], this is often referred to as the exact solution. Sometimes, you may be asked to give an approximation, which would be more useful to someone using the result for a financial, scientific or engineering application. The approximation for [latex]x={e}^{2}[/latex] can be found with a calculator. [latex]x={e}^{2}\approx{7.4}[/latex] In general, we can describe using the definition of a logarithm to solve logarithmic equations as follows:For any algebraic expression S and real numbers b and c, where [latex]b>0,\text{ }b\ne 1[/latex],
Example
Solve [latex]2\mathrm{ln}\left(6x\right)=7[/latex].Answer: [latex]\begin{array}{c}2\mathrm{ln}\left(6x\right)=7\hfill & \hfill \\ \text{ }\mathrm{ln}\left(6x\right)=\frac{7}{2}\hfill & \text{Divide by 2}.\hfill \\ \text{ }6x={e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{ }x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide by 6}.\hfill \end{array}[/latex]
Answer
Exact answer: [latex]x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}[/latex] Approximate answer: [latex]x\approx{5.5}[/latex]Example
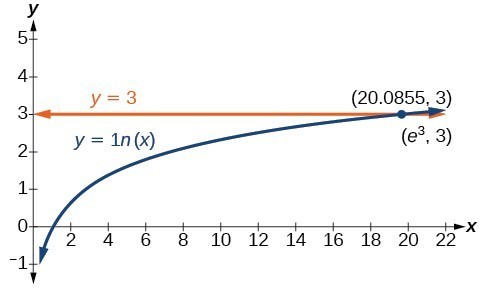
Solve [latex]\mathrm{ln}x=3[/latex].Answer:
[latex]\begin{array}{c}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of the natural logarithm}\text{.}\hfill \end{array}[/latex]
The graph below represents the graph of the equation. On the graph, the x-coordinate of the point at which the two graphs intersect is close to 20. In other words [latex]{e}^{3}\approx 20[/latex]. A calculator gives a better approximation: [latex]{e}^{3}\approx 20.0855[/latex].
Use the one-to-one property of logarithms to solve logarithmic equations
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers [latex]<em>x </em>> 0, <em>S </em>> 0, <em>T </em>> 0[/latex] and any positive real number b, where [latex]b\ne 1[/latex],
For example,
So, if [latex]x - 1=8[/latex], then we can solve for x, and we get [latex]<em>x </em>= 9[/latex]. To check, we can substitute [latex]<em>x </em>= 9[/latex] into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex]. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
Example
Solve [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex] Check your results.Answer: [latex]\begin{array}{c}\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{ }\mathrm{log}\left(\frac{3x - 2}{2}\right)=\mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{ }\frac{3x - 2}{2}=x+4\hfill & \text{Apply the one to one property of a logarithm}.\hfill \\ \text{ }3x - 2=2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{ }x=10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}[/latex]
To check the result, substitute [latex]<em>x </em>= 10[/latex] into [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex].
Answer
[latex-display]x = 10[/latex-display]- Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex].
- Use the one-to-one property to set the arguments equal.
- Solve the resulting equation, [latex]S = T[/latex], for the unknown.
Example
[latex-display]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex-display]Answer: [latex]\begin{array}{c}\text{ }\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)\hfill & \hfill \\ \text{ }{x}^{2}=2x+3\hfill & \text{Use the one-to-one property of the logarithm}.\hfill \\ \text{ }{x}^{2}-2x - 3=0\hfill & \text{Get zero on one side before factoring}.\hfill \\ \left(x - 3\right)\left(x+1\right)=0\hfill & \text{Factor using FOIL}.\hfill \\ \text{ }x - 3=0\text{ or }x+1=0\hfill & \text{If a product is zero, one of the factors must be zero}.\hfill \\ \text{ }x=3\text{ or }x=-1\hfill & \text{Solve for }x.\hfill \end{array}[/latex]
Analysis of the Solution
There are two solutions: [latex]<em>x </em>= 3 or <em>x </em>= –1[/latex]. The solution [latex]<em>x </em>= –1[/latex] is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.
Summary
We can combine the definitions of logarithms and algebraic tools used for solving linear equations to solve logarithmic equations. Graphing each side of a logarithmic equation helps you analyze the solution.Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
