Read: Graph Exponential Functions
Learning Objectives
- Generate a table of values for an exponential function
- Plot an exponential function on Cartesian axes
We learn a lot about things by seeing their pictorial representations, and that is exactly why graphing exponential equations is a powerful tool. It gives us another layer of insight for predicting future events. Before we begin graphing, it is helpful to review the behavior of exponential growth. Recall the table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is greater than one. We’ll use the function [latex]f\left(x\right)={2}^{x}[/latex]. Observe how the output values in the table below change as the input increases by [latex]1[/latex].
| x | [latex]–3[/latex] | [latex]–2[/latex] | [latex]–1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] |
| [latex]f\left(x\right)={2}^{x}[/latex] | [latex]\frac{1}{8}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{2}[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]4[/latex] | [latex]8[/latex] |
Each output value is the product of the previous output and the base, [latex]2[/latex]. We call the base [latex]2[/latex] the constant ratio. In fact, for any exponential function with the form [latex]f\left(x\right)=a{b}^{x}[/latex], b is the constant ratio of the function. This means that as the input increases by [latex]1[/latex], the output value will be the product of the base and the previous output, regardless of the value of a.
Notice from the table that
- the output values are positive for all values of x;
- as x increases, the output values increase without bound; and
- as x decreases, the output values grow smaller, approaching zero.
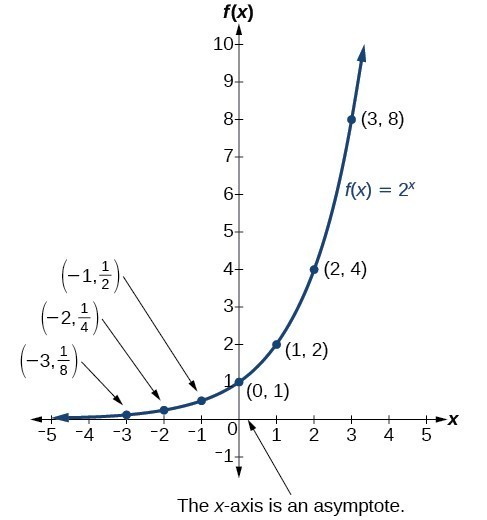 Notice that the graph gets close to the x-axis, but never touches it.
Notice that the graph gets close to the x-axis, but never touches it.The domain of [latex]f\left(x\right)={2}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex].
To get a sense of the behavior of exponential decay, we can create a table of values for a function of the form [latex]f\left(x\right)={b}^{x}[/latex] whose base is between zero and one. We’ll use the function [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex]. Observe how the output values in the table below change as the input increases by [latex]1[/latex].
| x | –[latex]3[/latex] | –[latex]2[/latex] | –[latex]1[/latex] | [latex]0[/latex] | [latex]1[/latex] | [latex]2[/latex] | [latex]3[/latex] |
| [latex]g\left(x\right)=\left(\frac{1}{2}\right)^{x}[/latex] | [latex]8[/latex] | [latex]4[/latex][/latex] | [latex]2[/latex] | [latex]1[/latex] | [latex]\frac{1}{2}[/latex] | [latex]\frac{1}{4}[/latex] | [latex]\frac{1}{8}[/latex] |
Again, because the input is increasing by [latex]1[/latex], each output value is the product of the previous output and the base, or constant ratio [latex]\frac{1}{2}[/latex].
Notice from the table that
- the output values are positive for all values of x;
- as x increases, the output values grow smaller, approaching zero; and
- as x decreases, the output values grow without bound.
The graph shows the exponential decay function, [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex].
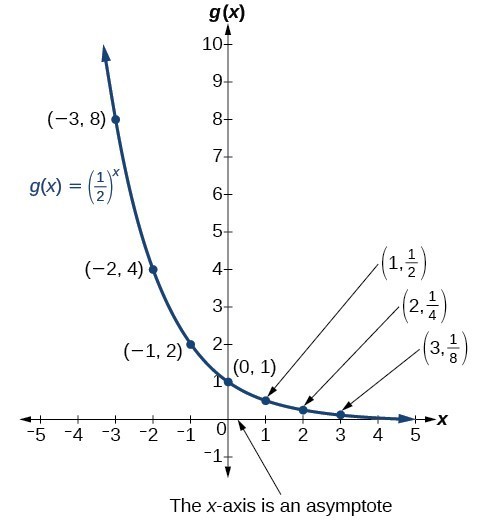
The domain of [latex]g\left(x\right)={\left(\frac{1}{2}\right)}^{x}[/latex] is all real numbers, the range is [latex]\left(0,\infty \right)[/latex]
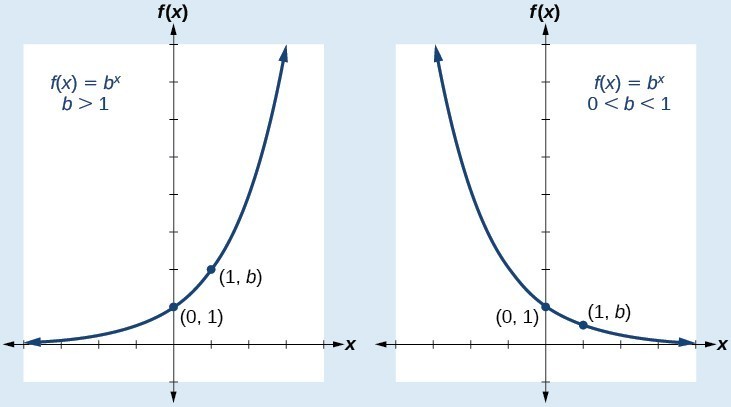
Characteristics of the Graph of f(x) = bx
An exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], [latex]b>0[/latex], [latex]b\ne 1[/latex], has these characteristics:
- one-to-one function
- domain: [latex]\left(-\infty , \infty \right)[/latex]
- range: [latex]\left(0,\infty \right)[/latex]
- x-intercept: none
- y-intercept: [latex]\left(0,1\right)[/latex]
- increasing if [latex]b>1[/latex]
- decreasing if [latex]b<1[/latex]
Compare the graphs of exponential growth and decay functions.
Example
Sketch a graph of [latex]f\left(x\right)={0.25}^{x}[/latex]. State the domain, range.Answer:
Before graphing, identify the behavior and create a table of points for the graph.
- Since b =[latex]0.25[/latex] is between zero and one, we know the function is decreasing, and we can verify this by creating a table of values. The left tail of the graph will increase without bound and the right tail will get really close to the x-axis.
- Create a table of points.
x [latex]–3[/latex] [latex]–2[/latex] [latex]–1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex] [latex]f\left(x\right)={0.25}^{x}[/latex] [latex]64[/latex] [latex]16[/latex] [latex]4[/latex] [latex]1[/latex] [latex]0.25[/latex] [latex]0.0625[/latex] [latex]0.015625[/latex] - Plot the y-intercept, [latex]\left(0,1\right)[/latex], along with two other points. We can use [latex]\left(-1,4\right)[/latex] and [latex]\left(1,0.25\right)[/latex].
Draw a smooth curve connecting the points.

The domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(0,\infty \right)[/latex].
How To: Given an exponential function of the form [latex]f\left(x\right)={b}^{x}[/latex], graph the function.
- Create a table of points.
- Plot at least [latex]3[/latex] point from the table, including the y-intercept [latex]\left(0,1\right)[/latex].
- Draw a smooth curve through the points.
- State the domain, [latex]\left(-\infty ,\infty \right)[/latex], the range, [latex]\left(0,\infty \right)[/latex].
Example
Sketch a graph of [latex]f(x)={\sqrt{2}(\sqrt{2})}^{x}[/latex]. State the domain, range.Answer:
Before graphing, identify the behavior and create a table of points for the graph.
- Since b = [latex]\sqrt{2}[/latex] which is greater than one, we know the function is increasing, and we can verify this by creating a table of values. The left tail of the graph will get really close to the x-axis and the right tail will increase without bound.
- Create a table of points.
x [latex]–3[/latex] [latex]–2[/latex] [latex]–1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex] [latex]f\left(x\right)=\sqrt{2}{(\sqrt{2})}^{x}[/latex] [latex]0.5[/latex] [latex]0.71[/latex] [latex]1[/latex] [latex]1.41[/latex] [latex]2[/latex] [latex]2.83[/latex] [latex]4[/latex] - Plot the y-intercept, [latex]\left(0,1.41\right)[/latex], along with two other points. We can use [latex]\left(-1,1\right)[/latex] and [latex]\left(1,2\right)[/latex].
Draw a smooth curve connecting the points.
 The domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(0,\infty \right)[/latex].
The domain is [latex]\left(-\infty ,\infty \right)[/latex]; the range is [latex]\left(0,\infty \right)[/latex].
Summary
Graphs of exponential growth functions will have a right tail that increases without bound, and a left tail that gets really close to the x-axis. On the other hand, graph so exponential decay functions will have a left tail that increases without bound and a right tail that gets really close to the x-axis. Points can be generated with a table of values and plotted on a set of cartesian axes.Licenses & Attributions
CC licensed content, Original
- Graph a Basic Exponential Function Using a Table of Values. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Graph an Exponential Function Using a Table of Values. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
