Read: Find Domain and Range From a Graph
Learning Objectives
- Define the domain of linear, quadratic, radical, and rational functions from graphs
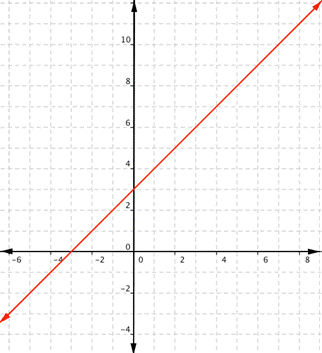 Any real number can be substituted for x and get a meaningful output. For any real number, you can always find an x value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range.
The domain and range are all real numbers.
For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.
Any real number can be substituted for x and get a meaningful output. For any real number, you can always find an x value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range.
The domain and range are all real numbers.
For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.
Example
What are the domain and range of the real-valued function [latex]f(x)=−3x^{2}+6x+1[/latex]?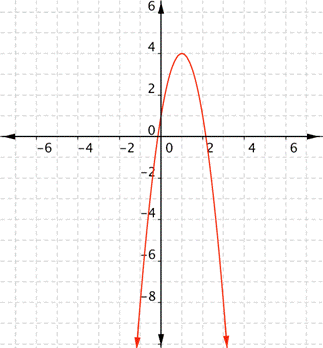
Answer: This is a quadratic function. There are no rational (divide by zero) or radical (negative number under a root) expressions, so there is nothing that will restrict the domain. Any real number can be used for x to get a meaningful output. Because the coefficient of [latex]x^{2}[/latex] is negative, it will open downward. With quadratic functions, remember that there is either a maximum (greatest) value, or a minimum (least) value. In this case, there is a maximum value. The vertex, or high point, is at ([latex]1, 4[/latex]). From the graph, you can see that [latex]f(x)\leq4[/latex].
Answer
The domain is all real numbers, and the range is all real numbers f(x) such that [latex]f(x)\leq4[/latex]. You can check that the vertex is indeed at ([latex]1, 4[/latex]). Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y value. The vertex must lie on the line of reflection, because it’s the only point that does not have a mirror image! In the previous example, notice that when [latex]x=2[/latex] and when [latex]x=0[/latex], the function value is [latex]1[/latex]. (You can verify this by evaluating [latex]f(2)[/latex] and [latex]f(0)[/latex].) That is, both ([latex]2, 1[/latex]) and ([latex]0, 1[/latex]) are on the graph. The line of reflection here is [latex]x=1[/latex], so the vertex must be at the point [latex](1, f(1))[/latex] . Evaluating f(1) gives [latex]f(1)=4[/latex], so the vertex is at [latex](1, 4)[/latex].Example
What is the domain and range of the real-valued function [latex]f(x)=-2+\sqrt{x+5}[/latex]?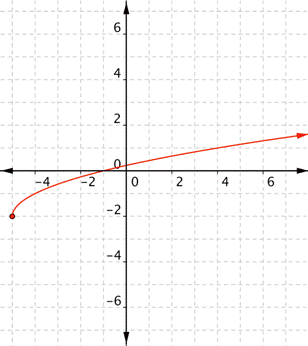
Answer: This is a radical function. The domain of a radical function is any x value for which the radicand (the value under the radical sign) is not negative. That means [latex]x+5\geq0[/latex], so [latex]x\geq−5[/latex]. Since the square root must always be positive or [latex]0[/latex], [latex] \displaystyle \sqrt{x+5}\ge 0[/latex]. That means [latex] \displaystyle -2+\sqrt{x+5}\ge -2[/latex].
Answer
The domain is all real numbers x where [latex]x\geq−5[/latex], and the range is all real numbers f(x) such that [latex]f(x)\geq−2[/latex].Example
What is the domain of the real-valued function [latex] \displaystyle f(x)=\frac{3x}{x+2}[/latex]?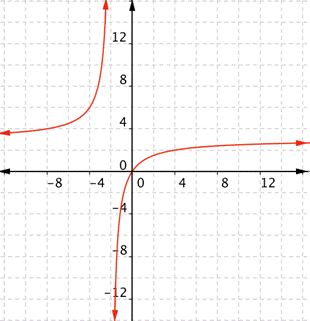
Answer: This is a rational function. The domain of a rational function is restricted where the denominator is [latex]0[/latex]. In this case, [latex]x+2[/latex] is the denominator, and this is [latex]0[/latex] only when [latex]x=−2[/latex].
Answer
The domain is all real numbers except [latex]−2[/latex]Summary
Although a function may be given as “real valued,” it may be that the function has restrictions to its domain and range. There may be some real numbers that can’t be part of the domain or part of the range. This is particularly true with rational and radical functions, which can have restrictions to domain, range, or both. Other functions, such as quadratic functions and polynomial functions of even degree, also can have restrictions to their range.Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 1: Determine the Domain and Range of the Graph of a Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
