Functions Practice Test
For the following exercises, determine whether each of the following relations is a function. 1. y = 2x + 8 2. [latex]\left\{\left(2,1\right),\left(3,2\right),\left(-1,1\right),\left(0,-2\right)\right\}\\[/latex] For the following exercises, evaluate the function [latex]f\left(x\right)=-3{x}^{2}+2x\\[/latex] at the given input. 3. [latex]f\left(-2\right)\\[/latex] 4. [latex]f\left(a\right)\\[/latex] 5. Show that the function [latex]f\left(x\right)=-2{\left(x - 1\right)}^{2}+3\\[/latex] is not one-to-one. 6. Write the domain of the function [latex]f\left(x\right)=\sqrt{3-x}\\[/latex] in interval notation. 7. Given [latex]f\left(x\right)=2{x}^{2}-5x\\[/latex], find [latex]f\left(a+1\right)-f\left(1\right)\\[/latex]. 8. Graph the function [latex]\begin{cases}f\left(x\right) & =x+1 & \text{ if }-2 < x < 3 \\ \text{ }& =-x & \text{ if }x\ge 3\end{cases}\\[/latex] 9. Find the average rate of change of the function [latex]f\left(x\right)=3 - 2{x}^{2}+x\\[/latex] by finding [latex]\frac{f\left(b\right)-f\left(a\right)}{b-a}\\[/latex]. For the following exercises, use the functions [latex]f\left(x\right)=3 - 2{x}^{2}+x\text{ and }g\left(x\right)=\sqrt{x}\\[/latex] to find the composite functions. 10. [latex]\left(g\circ f\right)\left(x\right)\\[/latex] 11. [latex]\left(g\circ f\right)\left(1\right)\\[/latex] 12. Express [latex]H\left(x\right)=\sqrt[3]{5{x}^{2}-3x}\\[/latex] as a composition of two functions, f and g, where [latex]\left(f\circ g\right)\left(x\right)=H\left(x\right)\\[/latex]. For the following exercises, graph the functions by translating, stretching, and/or compressing a toolkit function. 13. [latex]f\left(x\right)=\sqrt{x+6}-1\\[/latex] 14. [latex]f\left(x\right)=\frac{1}{x+2}-1\\[/latex] For the following exercises, determine whether the functions are even, odd, or neither. 15. [latex]f\left(x\right)=-\frac{5}{{x}^{2}}+9{x}^{6}\\[/latex] 16. [latex]f\left(x\right)=-\frac{5}{{x}^{3}}+9{x}^{5}\\[/latex] 17. [latex]f\left(x\right)=\frac{1}{x}\\[/latex] 18. Graph the absolute value function [latex]f\left(x\right)=-2|x - 1|+3\\[/latex]. 19. Solve [latex]|2x - 3|=17\\[/latex]. 20. Solve [latex]-|\frac{1}{3}x - 3|\ge 17\\[/latex]. Express the solution in interval notation. For the following exercises, find the inverse of the function. 21. [latex]f\left(x\right)=3x - 5\\[/latex] 22. [latex]f\left(x\right)=\frac{4}{x+7}\\[/latex] For the following exercises, use the graph of g shown below.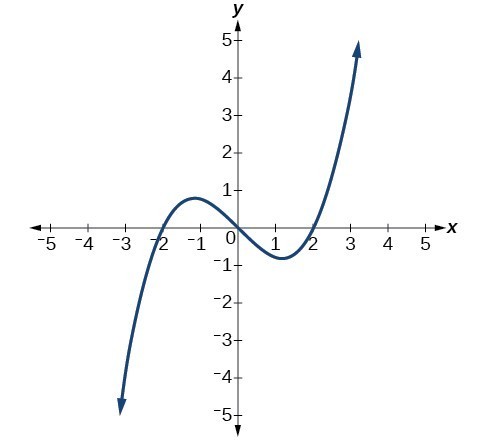 23. On what intervals is the function increasing?
24. On what intervals is the function decreasing?
25. Approximate the local minimum of the function. Express the answer as an ordered pair.
26. Approximate the local maximum of the function. Express the answer as an ordered pair.
For the following exercises, use the graph of the piecewise function shown below.
23. On what intervals is the function increasing?
24. On what intervals is the function decreasing?
25. Approximate the local minimum of the function. Express the answer as an ordered pair.
26. Approximate the local maximum of the function. Express the answer as an ordered pair.
For the following exercises, use the graph of the piecewise function shown below.
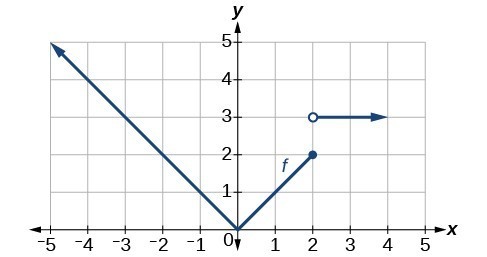 27. Find [latex]f\left(2\right)\\[/latex].
28. Find [latex]f\left(-2\right)\\[/latex].
29. Write an equation for the piecewise function.
For the following exercises, use the values listed below.
27. Find [latex]f\left(2\right)\\[/latex].
28. Find [latex]f\left(-2\right)\\[/latex].
29. Write an equation for the piecewise function.
For the following exercises, use the values listed below.
| x | F(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
| 8 | 17 |
Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
