We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Notation and Modeling Subtraction of Integers

Learning Outcomes

  • Model integer subtraction with color counters
You learn as a child how to subtract numbers through everyday experiences. For example, if you have 10 animal cookies and eat 6 of them, you will have 4 animal cookies left. Real-life experiences serve as models for subtracting positive numbers, and in some cases, such as temperature, for adding negative as well as positive numbers. But it is difficult to relate subtracting negative numbers to common life experiences. Most people do not have an intuitive understanding of subtraction when negative numbers are involved. Math teachers use several different models to explain subtracting negative numbers. We will continue to use counters to model subtraction. Remember, the blue counters represent positive numbers and the red counters represent negative numbers. Perhaps when you were younger, you read [latex]5 - 3[/latex] as five take away three. When we use counters, we can think of subtraction the same way. We will model four subtraction scenarios using the numbers [latex]5[/latex] and [latex]3[/latex].
  • [latex]5 - 3[/latex]
  • [latex]- 5-\left(-3\right)[/latex]
  • [latex]-5 - 3[/latex]
  • [latex]5-\left(-3\right)[/latex]

example

Model: [latex]5 - 3[/latex]. Solution:
Interpret the expression. [latex]5 - 3[/latex] means [latex]5[/latex] take away [latex]3[/latex] .
Model the first number. Start with [latex]5[/latex] positives. .
Take away the second number. So take away [latex]3[/latex] positives. .
Find the counters that are left. .
[latex]5 - 3=2[/latex] . The difference between [latex]5[/latex] and [latex]3[/latex] is [latex]2[/latex] .
Now you can try a similar problem.

try it

Model the expression: [latex-display]6 - 4[/latex-display]

Answer: This figure shows a row of 6 light pink circles, representing positive counters. The first four are circled. [latex-display]2[/latex-display]

  Model the expression: [latex-display]7 - 4[/latex-display]

Answer: This figure shows a row of 7 light pink circles representing positive counters. The first four counters are circled. [latex-display]3[/latex-display]

In teh previous example we subtracted [latex]3[/latex] positives from positive [latex]5[/latex]. Now we will subtract [latex]3[/latex] negatives from negative [latex]5[/latex]. Compare the results of this example to the previous example after you read through it.

example

Model: [latex]-5-\left(-3\right)[/latex]

Answer: Solution:

Interpret the expression. [latex]-5-\left(-3\right)[/latex] means [latex]-5[/latex] take away [latex]-3[/latex] .
Model the first number. Start with [latex]5[/latex] negatives. .
Take away the second number. So take away [latex]3[/latex] negatives. .
Find the number of counters that are left. .
[latex]-5-\left(-3\right)=-2[/latex] . The difference between [latex]-5[/latex] and [latex]-3[/latex] is [latex]-2[/latex] .

You can try a similar problem.

try it

Model the expression: [latex-display]-6-\left(-4\right)[/latex-display]

Answer: This figure shows a row of 6 dark pink circles, representing negative counters. The last four counters are circled. [latex-display]−2[/latex-display]

  Model the expression: [latex-display]-7-\left(-4\right)[/latex-display]

Answer: This figure is a row of 7 dark pink circles representing negative counters. The first four counters are circled. [latex-display]−3[/latex-display]

Notice that the previous two examples are very much alike.
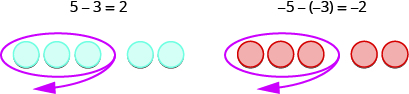
  • First, we subtracted [latex]3[/latex] positives from [latex]5[/latex] positives to get [latex]2[/latex] positives.
  • Then we subtracted [latex]3[/latex] negatives from [latex]5[/latex] negatives to get [latex]2[/latex] negatives.
Each example used counters of only one color, and the "take away" model of subtraction was easy to apply. This figure has a row of 5 blue circles. The first three are circled. Above the row is 5 minus 3 equals 2. Next to this is a row of 5 red circles. The first three are circled. Above the row is negative 5 minus negative 3 equals negative 2. Now let’s see what happens when we subtract one positive and one negative number. We will need to use both positive and negative counters and sometimes some neutral pairs, too. Adding a neutral pair does not change the value.

example

Model: [latex]-5 - 3[/latex].

Answer: Solution:

Interpret the expression. [latex]-5 - 3[/latex] means [latex]-5[/latex] take away [latex]3[/latex] .
Model the first number. Start with [latex]5[/latex] negatives. .
Take away the second number. So we need to take away [latex]3[/latex] positives.
But there are no positives to take away. Add neutral pairs until you have [latex]3[/latex] positives. .
Now take away [latex]3[/latex] positives. .
Count the number of counters that are left. .
[latex]-5 - 3=-8[/latex] . The difference of [latex]-5[/latex] and [latex]3[/latex] is [latex]-8[/latex] .

Now you can try a similar problem.

try it

Model the expression: [latex-display]-6 - 4[/latex-display]

Answer: This figure shows a row of 10 dark pink circles, representing negative counters. The first six counters are separated from the last four. Below the dark pink circles are four light pink circles, representing positive counters. These four positive counters are circled. [latex-display]−10[/latex-display]

  Model the expression: [latex-display]-7 - 4[/latex-display]

Answer: This figure shows a row of 11 dark pink circles, representing negative counters. The first seven counters are separated from the last four. Below the dark pink circles are four light pink circles, representing positive counters. These four positive counters are circled. [latex-display]−11[/latex-display]

Now we will subtract a negative number from a positive number. Think of this as taking away the negative.

example

Model: [latex]5-\left(-3\right)[/latex].

Answer: Solution:

Interpret the expression. [latex]5-\left(-3\right)[/latex] means [latex]5[/latex] take away [latex]-3[/latex] .
Model the first number. Start with [latex]5[/latex] positives. .
Take away the second number, so take away [latex]3[/latex] negatives.
But there are no negatives to take away. Add neutral pairs until you have [latex]3[/latex] negatives. .
Then take away [latex]3[/latex] negatives. .
Count the number of counters that are left. .
The difference of [latex]5[/latex] and [latex]-3[/latex] is [latex]8[/latex] . [latex]5-\left(-3\right)=8[/latex]

Now you can try a similar problem.

try it

Model the expression: [latex-display]6-\left(-4\right)[/latex-display]

Answer: This figure shows a row of 10 light pink circles, representing positive counters. The first six counters are separated from the last four. Below the light pink circles are four dark pink circles, representing negative counters. These four negative counters are circled. [latex-display]10[/latex-display]

  Model the expression: [latex-display]7-\left(-4\right)[/latex-display]

Answer: This figure shows a row of 11 light pink circles, representing positive counters. The first seven counters are separated from the last four. Below the light pink circles are four dark pink circles, representing negative counters. These four negative counters are circled. [latex-display]11[/latex-display]

  Now we will do an example that summarizes the situations above, with different numbers. Recall the different scenarios:
  • subtracting a positive number from a positive number
  • subtracting a positive number from a negative number
  • subtracting a negative number from a positive number
  • subtracting a negative number from a negative number

example

Model each subtraction. [latex-display]8 − 2[/latex-display] [latex-display]−5 − 4[/latex-display] [latex-display]6 − (−6)[/latex-display] [latex-display]−8 − (−3)[/latex-display]

Answer:

1.
[latex]8 - 2[/latex] This means [latex]8[/latex] take away [latex]2[/latex] .
Start with [latex]8[/latex] positives. .
Take away [latex]2[/latex] positives. .
How many are left? [latex]6[/latex]
[latex]8 - 2=6[/latex]
2.
[latex]-5 - 4[/latex] This means [latex]-5[/latex] take away [latex]4[/latex] .
Start with [latex]5[/latex] negatives. .
You need to take away [latex]4[/latex] positives. Add [latex]4[/latex] neutral pairs to get [latex]4[/latex] positives. . .
Take away [latex]4[/latex] positives. .
How many are left? .
[latex]-9[/latex]
[latex]-5 - 4=-9[/latex]
3.
[latex]6-\left(-6\right)[/latex] This means [latex]6[/latex] take away [latex]-6[/latex] .
Start with [latex]6[/latex] positives. .
Add [latex]6[/latex] neutrals to get [latex]6[/latex] negatives to take away. .
Remove [latex]6[/latex] negatives. .
How many are left? .
[latex]12[/latex]
[latex]6-\left(-6\right)=12[/latex]
4.
[latex]-8-\left(-3\right)[/latex] This means [latex]-8[/latex] take away [latex]-3[/latex] .
Start with [latex]8[/latex] negatives. .
Take away [latex]3[/latex] negatives. .
How many are left? .
[latex]-5[/latex]
[latex]-8-\left(-3\right)=-5[/latex]

Now you can try a similar problem.

try it

Model each subtraction. 1. [latex]7 - (-8)[/latex] 2. [latex]-2 - (-2)[/latex] 3. [latex]4 - 1[/latex] 4. [latex]-6 - 8[/latex]

Answer: 1. . 2. . 3. . 4. .

  Model each subtraction. 1. [latex]4 - (-6)[/latex] 2. [latex]-8 - (-1)[/latex] 3. [latex]7 - 3[/latex] 4. [latex]-4 - 2[/latex]

Answer: 1. . 2. . 3. . 4. .

Each of the examples so far have been carefully constructed so that the sign of the answer matched the sign of the first number in the expression.  For example, in  [latex]−5 − 4[/latex], the result is [latex]-9[/latex], which is the same sign as [latex]-5[/latex]. Now we will see subtraction where the sign of the result is different from the starting number.

example

Model each subtraction expression:
  1. [latex]2 - 8[/latex]
  2. [latex]-3-\left(-8\right)[/latex]

Answer: Solution

1. We start with [latex]2[/latex] positives. .
We need to take away [latex]8[/latex] positives, but we have only [latex]2[/latex].
Add neutral pairs until there are [latex]8[/latex] positives to take away. .
Then take away [latex]8[/latex] positives. .
Find the number of counters that are left. There are [latex]6[/latex] negatives. .
[latex]2 - 8=-6[/latex]
2. We start with [latex]3[/latex] negatives. .
We need to take away [latex]8[/latex] negatives, but we have only [latex]3[/latex].
Add neutral pairs until there are [latex]8[/latex] negatives to take away. .
Then take away the [latex]8[/latex] negatives. .
Find the number of counters that are left. There are [latex]5[/latex] positives. .
[latex]-3-\left(-8\right)=5[/latex]

Now you can try a similar problem.

try it

Model each subtraction expression.
  1. [latex]7 - 9[/latex]
  2. [latex]-5--9[/latex]

Answer: 1. This figure shows a row of 9 light pink circles, representing positive counters. The first seven are separated from the last two. The entire row is circled. Below the last two light pink circles is a row of two dark pink circles, representing negative counters. [latex-display]−2[/latex-display] 2. This figure shows a row of 9 dark pink circles, representing negative counters. The first five are separated from the last four. The entire row is circled. Below the last four dark pink circles is a row of four light pink circles, representing positive counters. [latex-display]4[/latex-display]

  Model each subtraction expression.
  1. [latex]4 - 7[/latex]
  2. [latex]-7-\left(-10\right)[/latex]

Answer: 1. This figure shows a row of seven light pink circles, representing positive counters. The first four are separated from the last three. The entire row is circled. Below the last three light pink circles is a row of three dark pink circles, representing negative counters. [latex-display]−3[/latex-display] 2. This figure shows a row of 10 dark pink circles, representing negative counters. The first seven are separated from the last three. The entire row is circled. Below the last three dark pink circles is a row of three light pink circles, representing positive counters. [latex-display]3[/latex-display]

When you subtract two integers, there are two possibilities, either the result will have a different sign from the starting number, or it will have the same sign. Watch the video below to see more examples of modeling integer subtraction with color counters. https://youtu.be/ZjiL7GfxgiI

Licenses & Attributions

CC licensed content, Shared previously

  • Subtracting Integers with Color Counters (No Extra Zeros Needed). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.

CC licensed content, Specific attribution