We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

학습 가이드 > Mathematics for the Liberal Arts

Set Theory Basics

It is natural for us to classify items into groups, or sets, and consider how those sets overlap with each other. We can use these sets understand relationships between groups, and to analyze survey data.

Introduction to Set Theory

An art collector might own a collection of paintings, while a music lover might keep a collection of CDs. Any collection of items can form a set.

Set

A set is a collection of distinct objects, called elements of the set A set can be defined by describing the contents, or by listing the elements of the set, enclosed in curly brackets.

Example

Some examples of sets defined by describing the contents:
  1. The set of all even numbers
  2. The set of all books written about travel to Chile

Answer: Some examples of sets defined by listing the elements of the set:

  1. {1, 3, 9, 12}
  2. {red, orange, yellow, green, blue, indigo, purple}

Notation

Commonly, we will use a variable to represent a set, to make it easier to refer to that set later. The symbol ∈ means “is an element of”. A set that contains no elements, { }, is called the empty set and is notated ∅

Example

Let A = {1, 2, 3, 4} To notate that 2 is element of the set, we’d write 2 ∈ A

Key Takeaways

Union, Intersection, and Complement

Commonly, sets interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.

Union, Intersection, and Complement

The union of two sets contains all the elements contained in either set (or both sets). The union is notated A ⋃ B. More formally, x ∊ A ⋃ B if x ∈ A or x ∈ B (or both) The intersection of two sets contains only the elements that are in both sets. The intersection is notated A ⋂ B. More formally, x ∈ A ⋂ B if x ∈ A and x ∈ B. The complement of a set A contains everything that is not in the set A. The complement is notated A’, or Ac, or sometimes ~A. A universal set is a set that contains all the elements we are interested in. This would have to be defined by the context. A complement is relative to the universal set, so Ac contains all the elements in the universal set that are not in A.
 

Example

  1. If we were discussing searching for books, the universal set might be all the books in the library.
  2. If we were grouping your Facebook friends, the universal set would be all your Facebook friends.
  3. If you were working with sets of numbers, the universal set might be all whole numbers, all integers, or all real numbers
 

Example

Suppose the universal set is U = all whole numbers from 1 to 9. If A = {1, 2, 4}, then Ac = {3, 5, 6, 7, 8, 9}.

Try It Now

Notice that in the example above, it would be hard to just ask for Ac, since everything from the color fuchsia to puppies and peanut butter are included in the complement of the set. For this reason, complements are usually only used with intersections, or when we have a universal set in place. As we saw earlier with the expression Ac ⋂ C, set operations can be grouped together. Grouping symbols can be used like they are with arithmetic – to force an order of operations.  

Example

Suppose H = {cat, dog, rabbit, mouse}, F = {dog, cow, duck, pig, rabbit}, and W = {duck, rabbit, deer, frog, mouse}
  1. Find (H ⋂ F) ⋃ W
  2. Find H ⋂ (F ⋃ W)
  3. Find (H ⋂ F)c ⋂ W

Answer:

  1. We start with the intersection: H ⋂ F = {dog, rabbit}. Now we union that result with W: (H ⋂ F) ⋃ W = {dog, duck, rabbit, deer, frog, mouse}
  2. We start with the union: F ⋃ W = {dog, cow, rabbit, duck, pig, deer, frog, mouse}. Now we intersect that result with H: H ⋂ (F ⋃ W) = {dog, rabbit, mouse}
  3. We start with the intersection: H ⋂ F = {dog, rabbit}. Now we want to find the elements of W that are not in H ⋂ F. (H ⋂ F)c ⋂ W = {duck, deer, frog, mouse}

Venn Diagrams

To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18th century. These illustrations now called Venn Diagrams.

Venn Diagram

A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Overlapping areas indicate elements common to both sets. Basic Venn diagrams can illustrate the interaction of two or three sets.

Example

Create Venn diagrams to illustrate A ⋃ B, A ⋂ B, and Ac ⋂ B A ⋃ B contains all elements in either set.

Answer: ab1 A ⋂ B contains only those elements in both sets – in the overlap of the circles. ab2 Ac will contain all elements not in the set A. Ac ⋂ B will contain the elements in set B that are not in set A. ab3

Example

Use a Venn diagram to illustrate (H ⋂ F)c ⋂ W

Answer: We’ll start by identifying everything in the set H ⋂ F 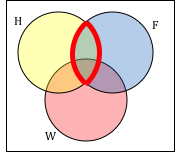hfw1 Now, (H ⋂ F)c ⋂ W will contain everything not in the set identified above that is also in set W. hfw2  

https://youtu.be/CPeeOUldZ6M

Example

Create an expression to represent the outlined part of the Venn diagram shown.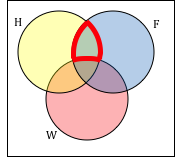 hfw3

Answer: The elements in the outlined set are in sets H and F, but are not in set W. So we could represent this set as H ⋂ F ⋂ Wc

Try It Now

Create an expression to represent the outlined portion of the Venn diagram shown. abc1
 

Exercises

What is the cardinality of P = the set of English names for the months of the year?

Answer: The cardinality of this set is 12, since there are 12 months in the year. Sometimes we may be interested in the cardinality of the union or intersection of sets, but not know the actual elements of each set. This is common in surveying.

 

Exercises

A survey asks 200 people “What beverage do you drink in the morning”, and offers choices:
  • Tea only
  • Coffee only
  • Both coffee and tea
Suppose 20 report tea only, 80 report coffee only, 40 report both.   How many people drink tea in the morning? How many people drink neither tea or coffee?

Answer: This question can most easily be answered by creating a Venn diagram. We can see that we can find the people who drink tea by adding those who drink only tea to those who drink both: 60 people. We can also see that those who drink neither are those not contained in the any of the three other groupings, so we can count those by subtracting from the cardinality of the universal set, 200. 200 – 20 – 80 – 40 = 60 people who drink neither. coffeetea

try it now

https://youtu.be/wErcETeKvrU

Licenses & Attributions

CC licensed content, Original

  • Mathematics for the Liberal Arts I. Provided by: Extended Learning Institute of Northern Virginia Community College Located at: https://online.nvcc.edu/. License: CC BY: Attribution.
  • Learning Objectives and Introduction. Provided by: Lumen Learning License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
  • Question ID 132343. Provided by: Lumen Learning License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Shared previously

  • Math in Society. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY-SA: Attribution-ShareAlike.
  • Question ID 132343. Provided by: Lumen Learning License: CC BY: Attribution.
  • Question ID 125855. Authored by: Bohart, Jenifer. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Sets: drawing a Venn diagram. Authored by: David Lippman. License: CC BY: Attribution.
  • Sets: drawing a Venn diagram. Authored by: David Lippman. License: CC BY: Attribution.
  • Question ID 6699. Authored by: Morales, Lawrence. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Sets: cardinality. Authored by: David Lippman. License: CC BY: Attribution.
  • Question ID 125872, 109842, 125878. Authored by: Bohart,Jenifer, mb Meacham,William. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.