We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra: Co-requisite Course

Graphs of Functions

Learning Objectives

  • Graph linear functions using a table of values
  • Graph a quadratic function using a table of values
  • Identify how multiplication can change the graph of a radical function
When both the input (independent variable) and the output (dependent variable) are real numbers, a function can be represented by a coordinate graph. The input is plotted on the horizontal x-axis and the output is plotted on the vertical y-axis. A helpful first step in graphing a function is to make a table of values. This is particularly useful when you don’t know the general shape the function will have. You probably already know that a linear function will be a straight line, but let’s make a table first to see how it can be helpful. When making a table, it’s a good idea to include negative values, positive values, and zero to ensure that you do have a linear function. Make a table of values for [latex]f(x)=3x+2[/latex]. Make a two-column table. Label the columns x and f(x).
x f(x)
Choose several values for x and put them as separate rows in the x column. These are YOUR CHOICE - there is no "right" or "wrong" values to pick, just go for it. Tip: It’s always good to include 0, positive values, and negative values, if you can.
x f(x)
[latex]−2[/latex]
[latex]−1[/latex]
[latex]0[/latex]
[latex]1[/latex]
[latex]3[/latex]
Evaluate the function for each value of x, and write the result in the f(x) column next to the x value you used. When [latex]x=0[/latex], [latex]f(0)=3(0)+2=2[/latex], [latex]f(1)=3(1)+2=5[/latex], [latex]f(−1)=3(−1)+2=−3+2=−1[/latex], and so on.
x f(x)
[latex]−2[/latex] [latex]−4[/latex]
[latex]−1[/latex] [latex]−1[/latex]
[latex]0[/latex] [latex]2[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]3[/latex] [latex]11[/latex]
(Note that your table of values may be different from someone else’s. You may each choose different numbers for x.) Now that you have a table of values, you can use them to help you draw both the shape and location of the function. Important: The graph of the function will show all possible values of x and the corresponding values of y. This is why the graph is a line and not just the dots that make up the points in our table. Graph [latex]f(x)=3x+2[/latex]. Using the table of values we created above you can think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid.
x f(x)
[latex]−2[/latex] [latex]−4[/latex]
[latex]−1[/latex] [latex]−1[/latex]
[latex]0[/latex] [latex]2[/latex]
[latex]1[/latex] [latex]5[/latex]
[latex]3[/latex] [latex]11[/latex]
Plot the points. The points negative 2, negative 4; the point negative 1, negative 1; the point 0, 2; the point 1, 5; the point 3, 11. Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge. A line through the points in the previous graph. Let’s try another one. Before you look at the answer, try to make the table yourself and draw the graph on a piece of paper.

Example

Graph [latex]f(x)=−x+1[/latex].

Answer: Start with a table of values. You can choose different values for x, but once again, it’s helpful to include 0, some positive values, and some negative values. If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid.

[latex]f(−2)=−(−2)+1=2+1=3\\f(−1)=−(−1)+1=1+1=2\\f(0)=−(0)+1=0+1=1\\f(1)=−(1)+1=−1+1=0\\f(2)=−(2)+1=−2+1=−1[/latex]

x f(x)
[latex]−2[/latex] [latex]3[/latex]
[latex]−1[/latex] [latex]2[/latex]
[latex]0[/latex] [latex]1[/latex]
[latex]1[/latex] [latex]0[/latex]
[latex]2[/latex] [latex]−1[/latex]
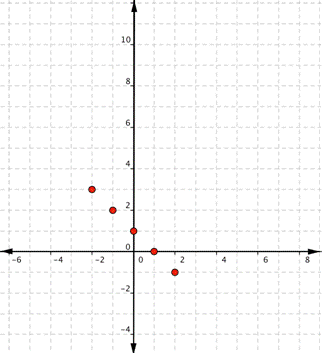
Plot the points. The point negative 2, 3; the point negative 1, 2; the point 0, 1; the point 1, 0; the point 2, negative 1.

Answer

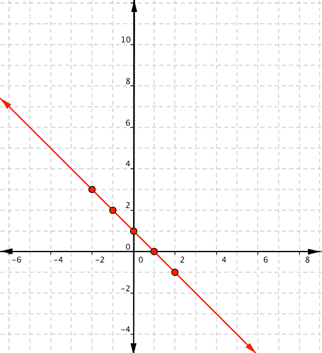Line through the points in the last graph. Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge.

In the following video we show another example of how to graph a linear function on a set of coordinate axes. https://youtu.be/sfzpdThXpA8 These graphs are representations of a linear function. Remember that a function is a correspondence between two variables, such as x and y. These will be discussed in further detail in the next module.

A General Note: Linear Function

A linear function is a function whose graph is a line. Linear functions can be written in the slope-intercept form of a line [latex-display]f\left(x\right)=mx+b[/latex-display] where [latex]b[/latex] is the initial or starting value of the function (when input, [latex]x=0[/latex]), and [latex]m[/latex] is the constant rate of change, or slope of the function. The y-intercept is at [latex]\left(0,b\right)[/latex].

Graph Quadratic Functions

Quadratic functions can also be graphed. It’s helpful to have an idea what the shape should be, so you can be sure that you’ve chosen enough points to plot as a guide. Let’s start with the most basic quadratic function, [latex]f(x)=x^{2}[/latex]. Graph [latex]f(x)=x^{2}[/latex]. Start with a table of values. Then think of the table as ordered pairs.
x f(x)
[latex]−2[/latex] [latex]4[/latex]
[latex]−1[/latex] [latex]1[/latex]
[latex]0[/latex] [latex]0[/latex]
[latex]1[/latex] [latex]1[/latex]
[latex]2[/latex] [latex]4[/latex]
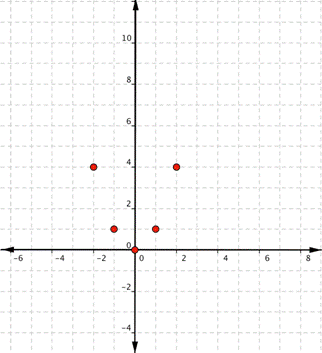Plot the points [latex](-2,4), (-1,1), (0,0), (1,1), (2,4)[/latex] Graph with the point negative 2, 4; the point negative 1, 1; the point 0, 0; the point 1,1; the point 2,4. Since the points are not on a line, you can’t use a straight edge. Connect the points as best you can, using a smooth curve (not a series of straight lines). You may want to find and plot additional points (such as the ones in blue here). Placing arrows on the tips of the lines implies that they continue in that direction forever. 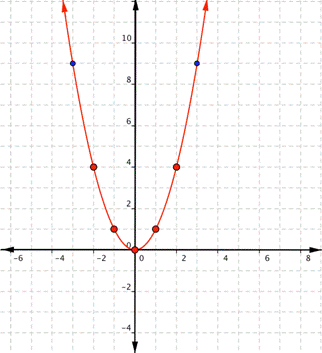A curved U-shaped line through the points from the previous graph. Notice that the shape is like the letter U. This is called a parabola. One-half of the parabola is a mirror image of the other half. The line that goes down the middle is called the line of reflection, in this case that line is they y-axis. The lowest point on this graph is called the vertex. In the following video we show an example of plotting a quadratic function using a table of values. https://youtu.be/wYfEzOJugS8 The equations for quadratic functions have the form [latex]f(x)=ax^{2}+bx+c[/latex] where [latex] a\ne 0[/latex]. In the basic graph above, [latex]a=1[/latex], [latex]b=0[/latex], and [latex]c=0[/latex]. Changing a changes the width of the parabola and whether it opens up ([latex]a>0[/latex]) or down ([latex]a<0[/latex]). If a is positive, the vertex is the lowest point, if a is negative, the vertex is the highest point. In the following example, we show how changing the value of a will affect the graph of the function.

Example

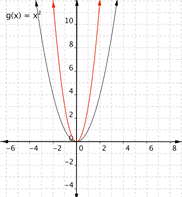
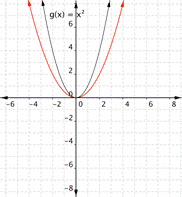
Match the following functions with their graph. a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex] b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/latex] c)[latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex] a)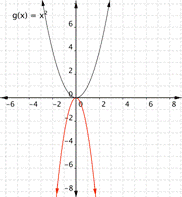 compared to g(x)=x squared b) compared to g(x)=x squared c) compared to g(x)=x squared

Answer: Function a) [latex] \displaystyle f(x)=3{{x}^{2}}[/latex] means that inputs are squared and then multiplied by three, so the outputs will be greater than they would have been for [latex]f(x)=x^2[/latex].  This results in a parabola that has been squeezed, so the graph b) is the best match for this function. compared to g(x)=x squared Function b) [latex] \displaystyle f(x)=-3{{x}^{2}}[/latex] means that inputs are squared and then multiplied by negative three, so the outputs will be greater than they would have been for [latex]f(x)=x^2[/latex] so graph a)  is the best match for this function. compared to g(x)=x squared Function c) [latex] \displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex] means that inputs are squared then multiplied by [latex]\frac{1}{2}[/latex], so the outputs are less than they would be for [latex]f(x)=x^2[/latex].  This results in a parabola that has been opened wider than[latex]f(x)=x^2[/latex]. Graph c) is the best match for this function. compared to g(x)=x squared

Answer

Function a) matches graph b) Function b) matches graph a) Function c) matches graph c)

If there is no b term, changing c moves the parabola up or down so that the y intercept is (0, c). In the next example we show how changes to c affect the graph of the function.

Example

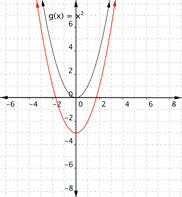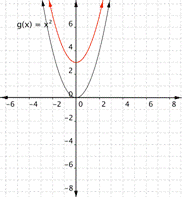
Match the following functions with their graph. a) [latex] \displaystyle f(x)={{x}^{2}}+3[/latex] b) [latex] \displaystyle f(x)={{x}^{2}}-3[/latex] a) compared to g(x)=x squared b) compared to g(x)=x squared

Answer: Function a) [latex] \displaystyle f(x)={{x}^{2}}+3[/latex] means square the inputs then add three, so every output will be moved up 3 units. the graph that matches this function best is b) compared to g(x)=x squared Function b) [latex] \displaystyle f(x)={{x}^{2}}-3[/latex]  means square the inputs then subtract three, so every output will be moved down 3 units. the graph that matches this function best is a) compared to g(x)=x squared

Licenses & Attributions

CC licensed content, Original

  • Graph a Quadratic Function Using a Table of Value and the Vertex. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Ex: Graph a Linear Function Using a Table of Values (Function Notation). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • Ex: Graph a Quadratic Function Using a Table of Values. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Determine if a Relation Given as a Table is a One-to-One Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 1: Use the Vertical Line Test to Determine if a Graph Represents a Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.