We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra CoRequisite Course

Express and Plot Complex Numbers

Learning Outcomes

  • Express square roots of negative numbers as multiples of [latex]i[/latex].
  • Plot complex numbers on the complex plane.
We know how to find the square root of any positive real number. In a similar way we can find the square root of a negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number [latex]i[/latex] is defined as the square root of negative 1.

[latex]\sqrt{-1}=i[/latex]

So, using properties of radicals,

[latex]{i}^{2}={\left(\sqrt{-1}\right)}^{2}=-1[/latex]

We can write the square root of any negative number as a multiple of [latex]i[/latex]. Consider the square root of –25.

[latex]\begin{align}\sqrt{-25}&=\sqrt{25\cdot \left(-1\right)}\\&=\sqrt{25}\cdot\sqrt{-1}\\ &=5i\end{align}[/latex]

We use [latex]5i[/latex] and not [latex]-\text{5}i[/latex] because the principal root of 25 is the positive root. A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written [latex]a+bi[/latex] where [latex]a[/latex] is the real part and [latex]bi[/latex] is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4\sqrt{3}i[/latex].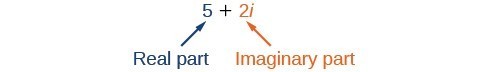 Showing the real and imaginary parts of 5 + 2i. In this complex number, 5 is the real part and 2i is the complex part. Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.

A General Note: Imaginary and Complex Numbers

A complex number is a number of the form [latex]a+bi[/latex] where
  • [latex]a[/latex] is the real part of the complex number.
  • [latex]bi[/latex] is the imaginary part of the complex number.
If [latex]b=0[/latex], then [latex]a+bi[/latex] is a real number. If [latex]a=0[/latex] and [latex]b[/latex] is not equal to 0, the complex number is called an imaginary number. An imaginary number is an even root of a negative number.

How To: Given an imaginary number, express it in standard form.

  1. Write [latex]\sqrt{-a}[/latex] as [latex]\sqrt{a}\cdot\sqrt{-1}[/latex].
  2. Express [latex]\sqrt{-1}[/latex] as i.
  3. Write [latex]\sqrt{a}\cdot i[/latex] in simplest form.

recall writing square roots in simplest form

Recall that the principal square root of [latex]a[/latex] is the nonnegative number that, when multiplied by itself, equals [latex]a[/latex]. It is written as a radical expression, with a symbol called a radical over the term called the radicand: [latex]\sqrt{a}[/latex].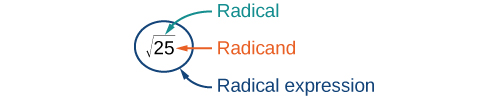 The expression: square root of twenty-five is enclosed in a circle. The circle has an arrow pointing to it labeled: Radical expression. The square root symbol has an arrow pointing to it labeled: Radical. The number twenty-five has an arrow pointing to it labeled: Radicand. To simplify a square root, we rewrite it such that there are no perfect squares in the radicand. Use the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite [latex]\sqrt{-75}[/latex] as [latex]\sqrt{25}\cdot \sqrt{3}\cdot \sqrt{-1} = 5  \sqrt{3}i[/latex].  

Example: Expressing an Imaginary Number in Standard Form

Express [latex]\sqrt{-9}[/latex] in standard form.

Answer: [latex-display]\sqrt{-9}=\sqrt{9}\cdot\sqrt{-1}=3i[/latex-display] In standard form, this is [latex]0+3i[/latex].

Try It

Express [latex]\sqrt{-24}[/latex] in standard form.

Answer: [latex-display]\sqrt{-24}=2i\sqrt{6}[/latex-display]

[ohm_question]61706[/ohm_question]
https://youtu.be/NeTRNpBI17I

Plot complex numbers on the complex plane

We cannot plot complex numbers on a number line as we might real numbers. However, we can still represent them graphically. To represent a complex number we need to address the two components of the number. We use the complex plane, which is a coordinate system in which the horizontal axis represents the real component and the vertical axis represents the imaginary component. Complex numbers are the points on the plane, expressed as ordered pairs [latex](a, b)[/latex], where [latex]a[/latex] represents the coordinate for the horizontal axis and [latex]b[/latex] represents the coordinate for the vertical axis.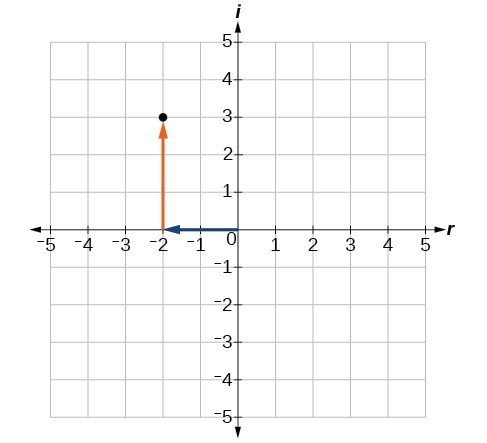 Plot of a complex number, -2 + 3i. Note that the real part (-2) is plotted on the x-axis and the imaginary part (3i) is plotted on the y-axis. Let’s consider the number [latex]-2+3i[/latex]. The real part of the complex number is [latex]–2[/latex] and the imaginary part is [latex]3i[/latex]. We plot the ordered pair [latex]\left(-2,3\right)[/latex] to represent the complex number [latex]-2+3i[/latex].

A General Note: Complex Plane

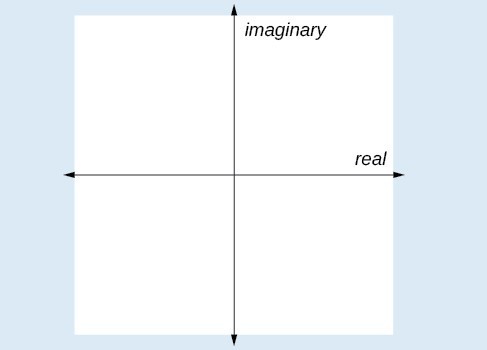The complex plane showing that the horizontal axis (in the real plane, the x-axis) is known as the real axis and the vertical axis (in the real plane, the y-axis) is known as the imaginary axis. In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis.

How To: Given a complex number, represent its components on the complex plane.

  1. Determine the real part and the imaginary part of the complex number.
  2. Move along the horizontal axis to show the real part of the number.
  3. Move parallel to the vertical axis to show the imaginary part of the number.
  4. Plot the point.

Example: Plotting a Complex Number on the Complex Plane

Plot the complex number [latex]3 - 4i[/latex] on the complex plane.

Answer: The real part of the complex number is [latex]3[/latex], and the imaginary part is [latex]–4i[/latex]. We plot the ordered pair [latex]\left(3,-4\right)[/latex]. Plot of a complex number, 3 - 4i. Note that the real part (3) is plotted on the x-axis and the imaginary part (-4i) is plotted on the y-axis.

Try It

Plot the complex number [latex]-4-i[/latex] on the complex plane.

Answer: Graph of the plotted point, -4-i.

[ohm_question]65079[/ohm_question]

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Introduction to Complex Numbers. Authored by: Sousa, James. License: CC BY: Attribution.
  • Question ID 61706. Authored by: Day, Alyson. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 65709. Authored by: Kaslik,Pete, mb Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].

CC licensed content, Specific attribution

  • College Algebra. Provided by: OpenStax Authored by: OpenStax College Algebra. License: CC BY: Attribution.