Read: Solve Compound Inequalities—AND
Learning Objectives
- Express solutions to inequalities graphically and with interval notation
- Identify solutions for compound inequalities in the form [latex]a<x<b[/latex], including cases with no solution
Solve compound inequalities in the form of and and express the solution graphically
The solution of a compound inequality that consists of two inequalities joined with the word and is the intersection of the solutions of each inequality. In other words, both statements must be true at the same time. The solution to an and compound inequality are all the solutions that the two inequalities have in common. As we saw in the last sections, this is where the two graphs overlap. TIP: When you are at a stop light and tell someone your location, you say, "I'm at the intersection of 2nd street and Paradise Lane. This is the part of the pavement that both roads have in common. Working a compound inequality is very similar to this. It's the part of the answers that both problems have in common. It's easier to see this intersection or overlap, if you graph both sets on the same number line. The overlapping region is your answer. If they don't overlap, there is no solution. In this section we will see more examples where we have to simplify the compound inequalities before we can express their solutions graphically or with an interval.Example
Solve for x. [latex] \displaystyle 1-4x\le 21\,\,\,\,\text{and}\,\,\,\,5x+2\ge22[/latex]Answer: Solve each inequality for x. Determine the intersection of the solutions.
[latex] \displaystyle \begin{array}{r}\,\,\,1-4x\le 21\,\,\,\,\,\,\,\,\text{AND}\,\,\,\,\,\,\,5x+2\ge 22\\\underline{-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,-2\,\,\,\,-2}\\\,\,\,\,\,\underline{-4x}\leq \underline{20}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{5x}\,\,\,\,\,\,\,\ge \underline{20}\\\,\,\,\,\,{-4}\,\,\,\,\,\,\,{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,x\ge -5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\ge 4\,\,\,\,\\\\x\ge -5\,\text{and}\,\,x\ge 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
The number line below shows the graphs of the two inequalities in the problem. The solution to the compound inequality is [latex]x\geq4[/latex], since this is where the two graphs overlap.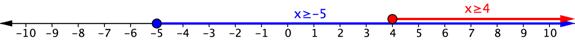
Answer
Inequality: [latex] \displaystyle x\ge 4[/latex] Interval: [latex]\left[4,\infty\right)[/latex] Graph: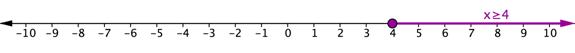
Example
Solve for x: [latex] \displaystyle {5}{x}-{2}\le{3}\text{ and }{4}{x}{+7}>{3}[/latex]Answer: Solve each inequality separately. Find the overlap between the solutions.
[latex] \displaystyle \begin{array}{l}\,\,\,5x-2\le 3\,\,\,\,\,\,\,\,\,\text{AND}\,\,\,\,\,\,\,4x+7>\,\,\,\,3\\\underline{\,\,\,\,\,\,\,\,\,\,\,+2\,\,+2\,}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,\,\,\,\,-7\,\,\,\,\,\,-7}\\\,\,\Large\frac{5x}{5}\,\,\,\,\,\,\,\,\le \frac{5}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{4x}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,>\frac{-4}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\le 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x>-1\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\le 1\,\,\,\,\text{and}\,\,\,\,x>-1\end{array}[/latex]
Answer
Inequality: [latex]-1<{x}\le{1}[/latex] Interval: [latex](-1,1][/latex] Graph:
Compound inequalities in the form [latex]a<x<b[/latex]
Rather than splitting a compound inequality in the form of [latex]a<x<b[/latex] into two inequalities [latex]x<b[/latex] and [latex]x>a[/latex], you can more quickly solve the inequality by applying the properties of inequality to all three segments of the compound inequality.Example
Solve for x. [latex]3\lt2x+3\leq 7[/latex]Answer: Isolate the variable by subtracting 3 from all 3 parts of the inequality, then dividing each part by 2.
[latex]\begin{array}{r}\,\,\,\,3\,\,\lt\,\,2x+3\,\,\leq \,\,\,\,7\\\underline{\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\underline{\,-3}\,\\\,\,\,\,\,\underline{\,0\,}\,\,\lt\,\,\,\,\underline{2x}\,\,\,\,\,\,\,\,\leq\,\,\,\underline{\,4\,}\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\\\,\,\,\,\,\,\,\,\,\,0\lt x\leq 2\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Answer
Inequality: [latex] \displaystyle 0\lt{x}\le 2[/latex] Interval: [latex]\left(0,2\right][/latex] Graph: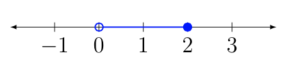
Example
Solve the compound inequality with variables in all three parts: [latex]3+x>7x - 2>5x - 10[/latex].Answer: Lets try the first method. Write two inequalities:

| Case 1: | |
|---|---|
| Description | The solution could be all the values between two endpoints |
| Inequalities | [latex]x\le{1}[/latex] and [latex]x\gt{-1}[/latex], or as a bounded inequality: [latex]{-1}\lt{x}\le{1}[/latex] |
| Interval | [latex]\left(-1,1\right][/latex] |
| Graphs |   |
| Case 2: | |
| Description | The solution could begin at a point on the number line and extend in one direction. |
| Inequalities | [latex]x\gt3[/latex] and [latex]x\ge4[/latex] |
| Interval | [latex]\left[4,\infty\right)[/latex] |
| Graphs |  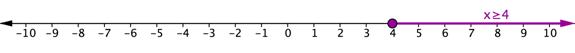 |
| Case 3: | |
| Description | In cases where there is no overlap between the two inequalities, there is no solution to the compound inequality |
| Inequalities | [latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex] |
| Intervals | [latex]\left(-\infty,-3\right)[/latex] and [latex]\left(3,\infty\right)[/latex] |
| Graph |  |
Example
Solve for x. [latex]x+2>5[/latex] and [latex]x+4<5[/latex]Answer: Solve each inequality separately.
[latex] \displaystyle \begin{array}{l}x+2>5\,\,\,\,\,\,\,\,\,\text{AND}\,\,\,\,\,\,\,x+4<5\,\,\,\,\\\underline{\,\,\,\,\,-2\,-2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-4\,-4}\\x\,\,\,\,\,\,\,\,>\,\,3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,<\,1\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,x>3\,\,\,\,\text{and}\,\,\,\,x<1\end{array}[/latex]
Find the overlap between the solutions.
Answer
There is no overlap between [latex] \displaystyle x>3[/latex] and [latex]x<1[/latex], so there is no solution.Summary
A compound inequality is a statement of two inequality statements linked together either by the word or or by the word and. Sometimes, an and compound inequality is shown symbolically, like [latex]a<x<b[/latex], and does not even need the word and. Because compound inequalities represent either a union or intersection of the individual inequalities, graphing them on a number line can be a helpful way to see or check a solution. Compound inequalities can be manipulated and solved in much the same way any inequality is solved, by paying attention to the properties of inequalities and the rules for solving them.Licenses & Attributions
CC licensed content, Shared previously
- Ex 1: Solve a Compound Inequality Involving AND (Intersection). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
- College Algebra. Provided by: OpenStax Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.
