Example

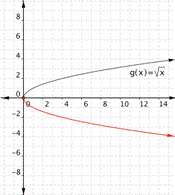
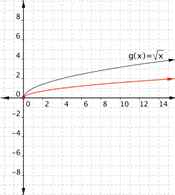
Match each of the following functions to the graph that it represents. a) [latex]f(x)=-\sqrt{x}[/latex] b)[latex]f(x)=2\sqrt{x}[/latex] c) [latex]f(x)=\dfrac{1}{2}\sqrt{x}[/latex] a)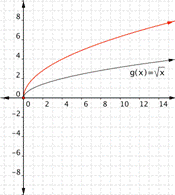 b) c)

Answer: Function a) [latex]f(x)=-\sqrt{x}[/latex] means that all the outputs will be negative - the function is the negative of the square roots of the input.  This will give the other half of the parabola on it's side.  Therefore the graph goes with the function [latex]f(x)=-\sqrt{x}[/latex]   Function b)[latex]f(x)=2\sqrt{x}[/latex] means take the square root of all the inputs, then multiply by two, so the outputs will be larger than the outputs for [latex]\sqrt{x}[/latex].  The graph goes with the function [latex]f(x)=2\sqrt{x}[/latex] Function c) [latex]f(x)=\dfrac{1}{2}\sqrt{x}[/latex] means take the squat=re root of the inputs then multiply by [latex]\Large\frac{1}{2}[/latex]. The outputs will be smaller than the outputs for [latex]\sqrt{x}[/latex]. The graph goes with the function [latex]f(x)=\dfrac{1}{2}\sqrt{x}[/latex].

Answer

Function a) goes with graph b) Function b) goes with graph a) Function c) goes with graph c)

Example

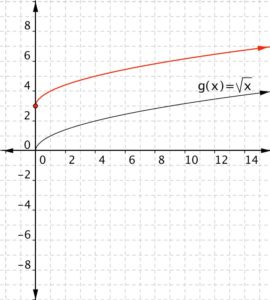
Match each of the following functions to the graph that it represents. a) [latex] f(x)=\sqrt{x}+3[/latex] b)[latex] f(x)=\sqrt{x}-2[/latex] a)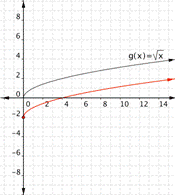 b)            

Answer: Function a) [latex] f(x)=\sqrt{x}+3[/latex] means take the square root of all the inputs and add three, so the out puts will be greater than those for [latex]\sqrt{x}[/latex], therefore the graph that goes with this function is             Function b) [latex]f(x)=\sqrt{x}-2[/latex] means take the square root of the input then subtract two. The outputs will be less than those for [latex]\sqrt{x}[/latex], therefore the graph that goes with this function is          

Answer

Function a) goes with graph b) Function b) goes with graph a)

Example

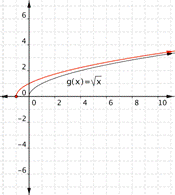
Match each of the following functions to the graph that it represents. a) [latex]f(x)=\sqrt{x+1}[/latex] b)[latex]f(x)=\sqrt{x-2}[/latex] a)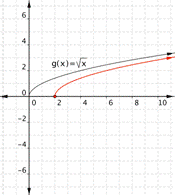 b)

Answer: Function a) [latex]f(x)=\sqrt{x+1}[/latex] adds one to the inputs before the square root is taken.  The outputs will be greater, so it ends up looking like a shift to the left. The graph that matches this function is Function b) [latex]f(x)=\sqrt{x-2}[/latex] means subtract before the square root is taken.  This makes the outputs less than they would be for the standard [latex]\sqrt{x}[/latex], and looks like a shift to the right. the graph that matches this function is

Answer

Function a) matches graph b) Function b) matches graph a)

Example

Graph [latex] f(x)=-2+\sqrt{x-1}[/latex].

Answer: Before making a table of values, look at the function equation to get a general idea what the graph should look like. Inside the square root, you’re subtracting [latex]1[/latex], so the graph will move to the right [latex]1[/latex] from the basic [latex] f(x)=\sqrt{x}[/latex] graph. You’re also adding [latex]−2[/latex] outside the square root, so the graph will move down two from the basic [latex] f(x)=\sqrt{x}[/latex] graph. Create a table of values. Choose values that will make your calculations easy. You want [latex]x–1[/latex] to be a perfect square ([latex]0, 1, 4, 9[/latex], and so on) so you can take the square root.

x	f(x)
[latex]1[/latex]	[latex]−2[/latex]
[latex]2[/latex]	[latex]−1[/latex]
[latex]5[/latex]	[latex]0[/latex]
[latex]10[/latex]	[latex]1[/latex]

Since values of x less than [latex]1[/latex] makes the value inside the square root negative, there will be no points on the coordinate graph to the left of [latex]x=1[/latex]. There is no need to choose x values less than [latex]1[/latex] for your table! Use the table pairs to plot points. Connect the points as best you can, using a smooth curve.

Answer