We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Putting it Together: Graph Linear Equations and Inequalities

Watercolor painting/sketch of a Joan's uncle Devon is a semiprofessional blogger who writes about media (he'd really like to be a paid film critic, but no one has offered yet). Recently, Devon posted a short blog piece complaining about the number of ads on TV these days, compared to when he was younger. He wasn't very scientific about it, and a couple of his readers disputed a claim he made and tried to start an argument. Devon asks Joan, who is taking an algebra class at night, to help him gather and cite some data to support his claim that there are "way more" TV ads now than when he was a kid. Together, they get online and do a little research, and find a website that reports some interesting data on the number of minutes of TV commercials per hour since 2009, shown below:
Years since 2009 Minutes
[latex]0[/latex] [latex]8.5[/latex]
[latex]1[/latex] [latex]9.25[/latex]
[latex]2[/latex] [latex]10[/latex]
[latex]3[/latex] [latex]10.75[/latex]
[latex]4[/latex] [latex]11.5[/latex]
[latex]5[/latex] [latex]12.25[/latex]
[latex]6[/latex] [latex]13[/latex]
The data show that, yes, there are more commercials now than in [latex]2009[/latex]. Joan decides the table isn't very exciting, because of the success she had with her manager when she reported her increase in sales using a graph. Also, Devon doubts that his readers will actually read a table. He agrees that a graph is the perfect thing to post on his blog to convince his skeptical readers! They get to work. First they  figure out what information they need to draw a graph of the line that represents the change in the number of minutes of commercials in one hour of TV since [latex]2009[/latex]?

The Cartesian Coordinate Plane

Joan remembers that the coordinate plane gives graphs structure and meaning. A straight line on a page won't tell Devon's readers much. Joan draws the axes and labels the horizontal one "Years Since [latex]2009[/latex]," because that's the first data point they have.  Then Devon labels the vertical axis from [latex]1[/latex] to [latex]18[/latex] because the minute data ranges from [latex]8.5[/latex] to [latex]13[/latex] minutes, and that will give room on either side.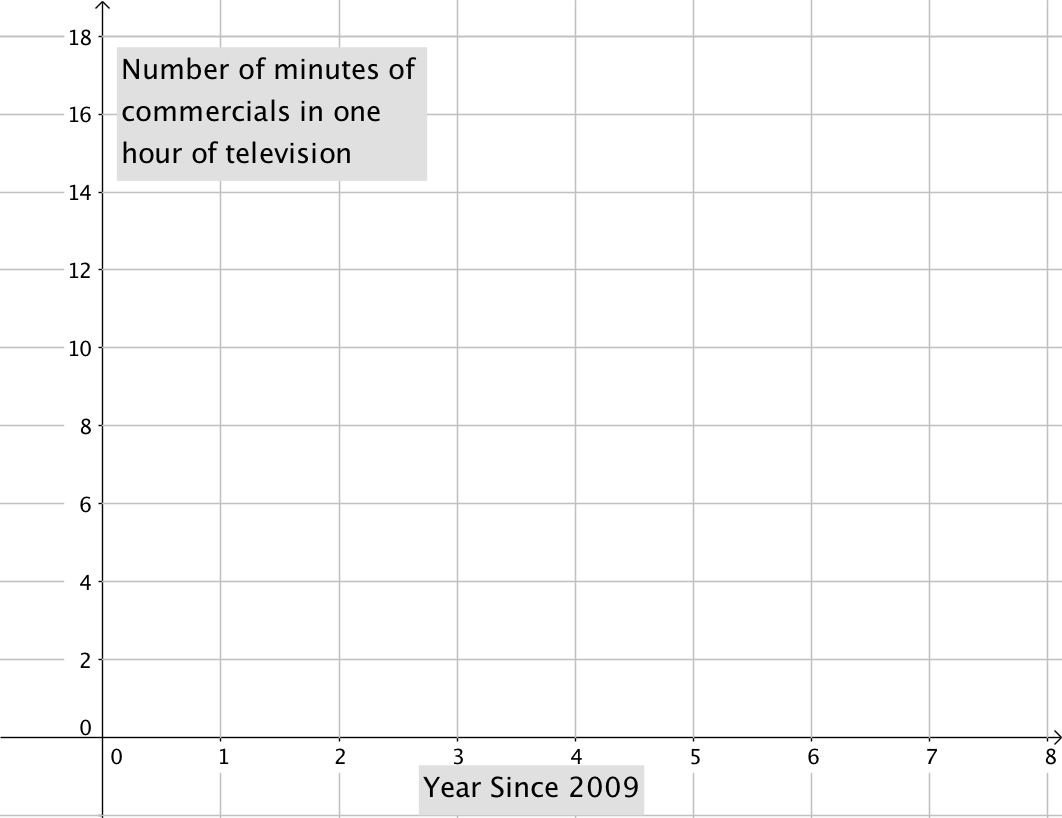 A graph, with the y-axis representing the number of minutes of commercials in one hour of television and the x-axis representing years since 2009. The y-axis is numbered 0 through 18 by twos, and the x-axis is labeled 0 through 8 by ones. They plot the ordered pairs from the table of values on the coordinate plane, as below. 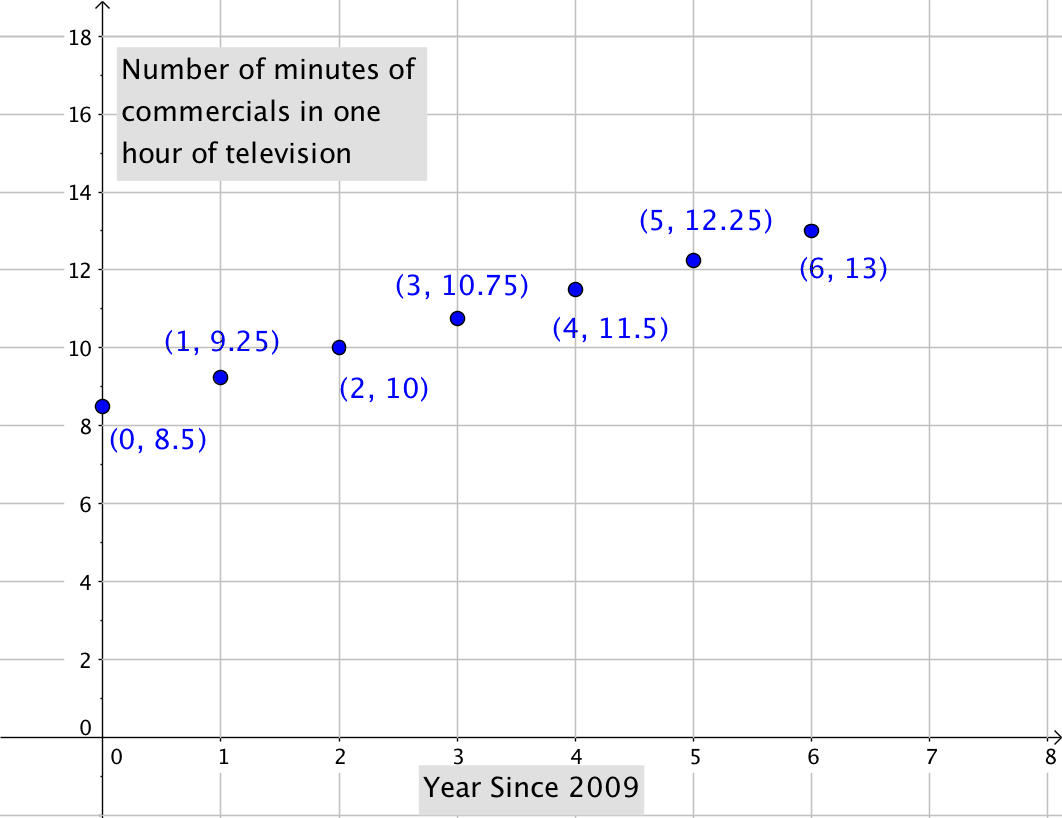The previous graph, with added points: the point (0,8.5), the point (1, 9.25), the point (2,10), the point (3,10.75), the point (4,11.5), the point (5,12.25), and the point (6,13). The points give them a guide for drawing the line, which is shown below. 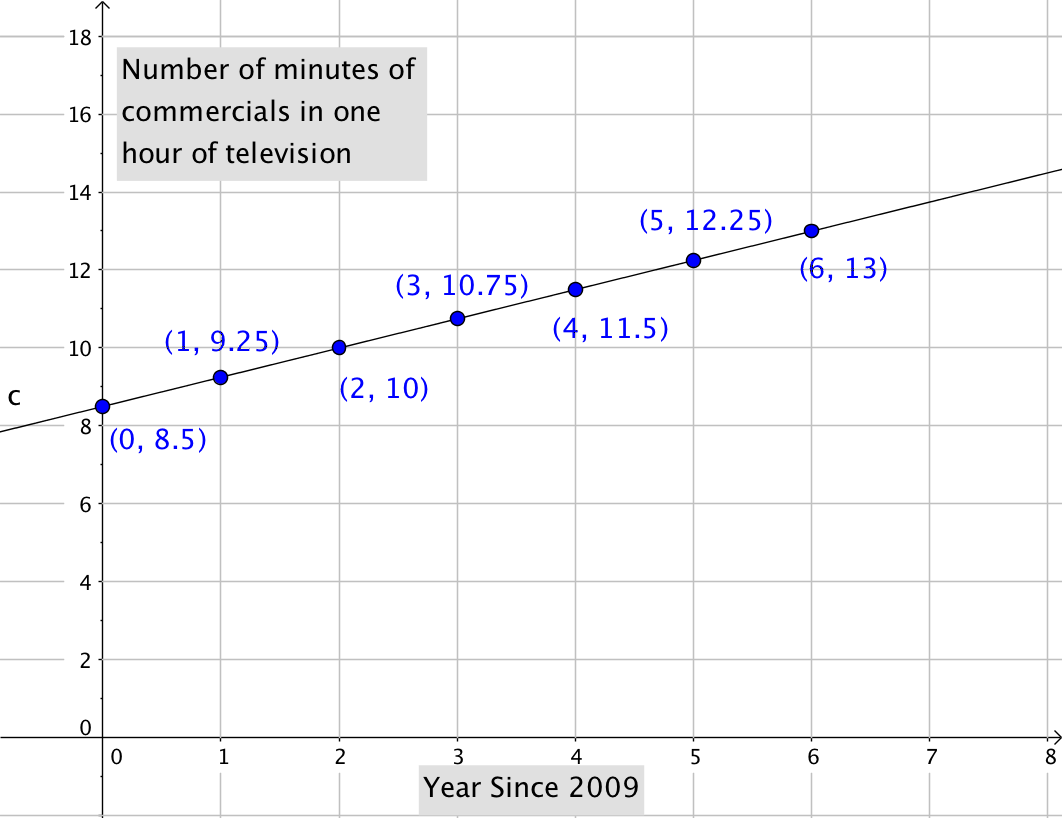An upward-sloping line drawn through the point (0,8.5), the point (1, 9.25), the point (2,10), the point (3,10.75), the point (4,11.5), the point (5,12.25), and the point (6,13). Devon is excited to post the graph on his blog to show people how much more time they are being exposed to commercials in one hour of TV watching since [latex]2009[/latex]. Then, it happens . . . One of his readers asks if he can guess how many minutes of commercials will be in one hour of television ten years from now (assuming the current trend continues). After thinking about the question for a while, Joan realizes they don't have to guess!  Joan and Devon have all the information they need to write the equation of the line they drew. She tells Devon that he could then put in any value for the years since [latex]2009[/latex].

Finding the Equation

Joan remembers that knowing the slope and y-intercept of a line can help her write the equation of the line.  She realizes they know the y-intercept: [latex](0,8.5)[/latex], and just need the slope. Joan checks her math notes to find the definition of slope, and uses two data points to calculate it:

[latex]\begin{array}{l} \text{Slope}=\dfrac{\text{rise}}{\text{run}}\\\\m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\\\\m=\dfrac{{11.5}-{10.75}}{{4}-{3}}\\\\m=\dfrac{{0.75}}{{1}} = 0.75\end{array}[/latex]

Now Devon and Joan have the two pieces of information they need to write the equation of the line that represents how many minutes of commercials will be in one hour of TV in any year before or after [latex]2009[/latex]. First, they choose some variables: x = the year and y = the number of minutes. They then substitute the values for m and b into the slope-intercept form of a line:

[latex]\begin{array}{l}{ y }= {m x} + {b}\\{ y }= {0.75 x} + {8.5}\end{array}[/latex]

Remembering that the whole point of this exercise was to answer Devon's reader's question, they then figure out what [latex]10[/latex] years from now would be in relation to [latex]0[/latex] representing [latex]2009[/latex] on your graph.  If [latex]10[/latex] years from now is [latex]2026[/latex], then it's [latex]17[/latex] years from [latex]2009[/latex].  The x value they need in order to answer the question is [latex]17[/latex].

[latex]\begin{array}{l}{ y }= {0.75 (17)} + {8.5}\\\\{ y }= {12.75} + {8.5}\\\\{ y }= {21.25}\end{array}[/latex]

Devon and Joan have a new data point: [latex](17,21.25)[/latex].  This means that in [latex]2026[/latex] there will be more than [latex]20[/latex] minutes of commercials in one hour of TV. Yuck!