We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Define and Evaluate Exponential Functions

Learning Objectives

  • Define an exponential function and it's domain and range
  • Evaluate an exponential function
  • Define and evaluate a compound interest formula
Linear functions have a constant rate of change – a constant number that the output increases for each increase in input. For example, in the equation [latex]f(x)=3x+4[/latex] , the slope tells us the output increases by three each time the input increases by one. Sometimes, on the other hand, quantities grow by a percent rate of change rather than by a fixed amount. In this lesson, we will define a function whose rate of change increases by a percent of the current value rather than a fixed quantity. To illustrate this difference consider two companies whose business is expanding: Company A has [latex]100[/latex] stores, and expands by opening [latex]50[/latex] new stores a year Company B has [latex]100[/latex] stores, and expands by increasing the number of stores by [latex]50\%[/latex] of their total each year. The table below compares the growth of each company where company A increases the number of stores linearly, and company B increases the number of stores by a rate of [latex]50\%[/latex] each year.
Year Stores, Company A  Description of Growth Stores, Company B
[latex]0[/latex] [latex]100[/latex] Starting with [latex]100[/latex] each [latex]100[/latex]
[latex]1[/latex] [latex]100+50=150[/latex] They both grow by [latex]50[/latex] stores in the first year. [latex]100[/latex] +[latex]50\%[/latex] of [latex]100 100 + 0.50(100) = 150[/latex]
[latex]2[/latex] [latex]150+50=200[/latex] Store A grows by [latex]50[/latex], Store B grows by [latex]75[/latex] [latex]150[/latex][latex]+ 50\%[/latex] of [latex]150 150 + 0.50(150) = 225[/latex]
[latex]3[/latex] [latex]200+50=250[/latex] Store A grows by [latex]50[/latex], Store B grows by [latex]112.5[/latex]  [latex]225 + 50\%[/latex] of [latex]225 225 + 0.50(225) = 337.5[/latex]
Company A has [latex]100[/latex] stores and expands by opening [latex]50[/latex] new stores a year, so its growth can be represented by the function [latex]A\left(x\right)=100+50x[/latex]. Company B has [latex]100[/latex] stores and expands by increasing the number of stores by [latex]50\%[/latex] each year, so its growth can be represented by the function [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex]. The graphs comparing the number of stores for each company over a five-year period are shown in below. We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
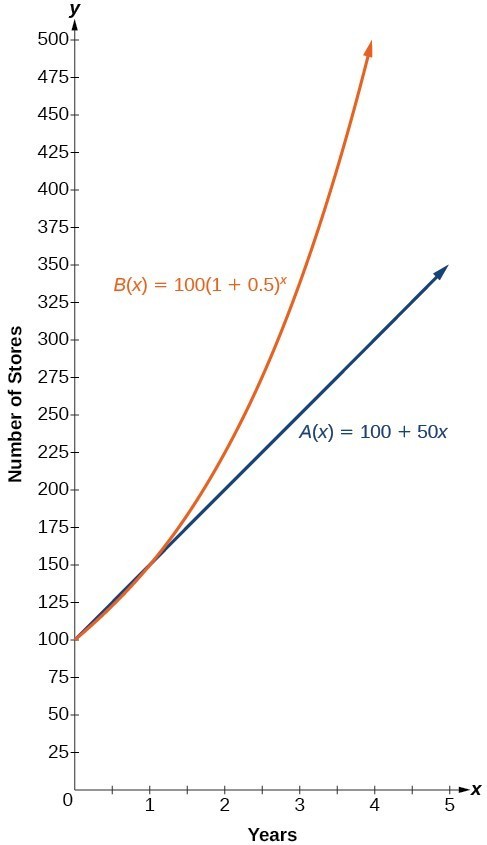Graph of Companies A and B’s functions, which values are found in the previous table. The graph shows the numbers of stores Companies A and B opened over a five-year period.

Notice that the domain for both functions is [latex]\left[0,\infty \right)[/latex], and the range for both functions is [latex]\left[100,\infty \right)[/latex]. After year [latex]1[/latex], Company B always has more stores than Company A.

Consider the function representing the number of stores for Company B

[latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex]

In this exponential function, [latex]100[/latex] represents the initial number of stores, [latex]0.50[/latex] represents the growth rate, and [latex]1+0.5=1.5[/latex] represents the growth factor. Generalizing further, we can write this function as [latex]B\left(x\right)=100{\left(1.5\right)}^{x}[/latex], where [latex]100[/latex] is the initial value, [latex]1.5[/latex] is called the base, and x is called the exponent. This is an exponential function.

Exponential Growth

A function that models exponential growth grows by a rate proportional to the current amount. For any real number x and any positive real numbers a and b such that [latex]b\ne 1[/latex], an exponential growth function has the form

[latex]f\left(x\right)=a{b}^{x}[/latex]

where

  • a is the initial or starting value of the function.
  • b is the growth factor or growth multiplier per unit x.

To evaluate an exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], we simply substitute x with the given value, and calculate the resulting power. For example:

Let [latex]f\left(x\right)={2}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?

[latex]\begin{array}{c}f\left(x\right)\hfill & ={2}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & ={2}^{3}\text{ }\hfill & \text{Substitute }x=3.\hfill \\ \hfill & =8\text{ }\hfill & \text{Evaluate the power}\text{.}\hfill \end{array}[/latex]

To evaluate an exponential function with a form other than the basic form, it is important to follow the order of operations. For example:

Let [latex]f\left(x\right)=30{\left(2\right)}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?

[latex]\begin{array}{c}f\left(x\right)\hfill & =30{\left(2\right)}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & =30{\left(2\right)}^{3}\hfill & \text{Substitute }x=3.\hfill \\ \hfill & =30\left(8\right)\text{ }\hfill & \text{Simplify the power first}\text{.}\hfill \\ \hfill & =240\hfill & \text{Multiply}\text{.}\hfill \end{array}[/latex]

Note that if the order of operations were not followed, the result would be incorrect:

[latex]f\left(3\right)=30{\left(2\right)}^{3}\ne {60}^{3}=216,000[/latex]
In our first example we will evaluate an exponential function without the aid of a calculator.

Example

Let [latex]f\left(x\right)=5{\left(3\right)}^{x+1}[/latex]. Evaluate [latex]f\left(2\right)[/latex] without using a calculator.

Answer:

Follow the order of operations. Be sure to pay attention to the parentheses.

[latex]\begin{array}{c}f\left(x\right)\hfill & =5{\left(3\right)}^{x+1}\hfill & \hfill \\ f\left(2\right)\hfill & =5{\left(3\right)}^{2+1}\hfill & \text{Substitute }x=2.\hfill \\ \hfill & =5{\left(3\right)}^{3}\hfill & \text{Add the exponents}.\hfill \\ \hfill & =5\left(27\right)\hfill & \text{Simplify the power}\text{.}\hfill \\ \hfill & =135\hfill & \text{Multiply}\text{.}\hfill \end{array}[/latex]

In the following video we present more examples of evaluating an exponential function at several different values. https://youtu.be/QFFAoX0We34 In the next example we will revisit the population of India.

Example

At the beginning of this section, we learned that the population of India was about [latex]1.25[/latex] billion in the year [latex]2013[/latex], with an annual growth rate of about [latex]1.2\%[/latex]. This situation is represented by the growth function [latex]P\left(t\right)=1.25{\left(1.012\right)}^{t}[/latex], where t is the number of years since [latex]2013[/latex]. To the nearest thousandth, what will the population of India be in [latex]2031[/latex]?

Answer:

To estimate the population in [latex]2031[/latex], we evaluate the models for  [latex]<em>t </em>= 18[/latex], because [latex]2031[/latex] is [latex]18[/latex] years after [latex]2013[/latex]. Rounding to the nearest thousandth,

[latex]P\left(18\right)=1.25{\left(1.012\right)}^{18}\approx 1.549[/latex]

There will be about [latex]1.549[/latex] billion people in India in the year [latex]2031[/latex].

In the following video we show another example of using an exponential function to predict the population of a small town. https://youtu.be/SbIydBmJePE You may have seen formulas that are used to calculate compound interest rates.  These formulas are another example of exponential growth. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.

The annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account. The term nominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than once a year, the effective interest rate ends up being greater than the nominal rate! This is a powerful tool for investing.

We can calculate the compound interest using the compound interest formula, which is an exponential function of the variables time t, principal P, APR r, and number of compounding periods in a year n:

[latex]A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt}[/latex]

The Compound Interest Formula

Compound interest can be calculated using the formula

[latex]A\left(t\right)=P{\left(1+\frac{r}{n}\right)}^{nt}[/latex]

where

  • A(t) is the account value,
  • t is measured in years,
  • P is the starting amount of the account, often called the principal, or more generally present value,
  • r is the annual percentage rate (APR) expressed as a decimal, and
  • n is the number of compounding periods in one year.
In our next example we will calculate the value of an account after [latex]10[/latex] years of interest compounded quarterly.

Example

If we invest [latex]$3,000[/latex] in an investment account paying [latex]3\%[/latex] interest compounded quarterly, how much will the account be worth in [latex]10[/latex] years?

Answer:

Because we are starting with [latex]$3,000[/latex], P = [latex]300[/latex]. Our interest rate is [latex]3\%[/latex], so r = [latex]0.03[/latex]. Because we are compounding quarterly, we are compounding [latex]4[/latex] times per year, so n = [latex]4[/latex]. We want to know the value of the account in [latex]10[/latex] years, so we are looking for A [latex](10)[/latex], the value when t = [latex]10[/latex].

[latex]\begin{array}{c}A\left(t\right)\hfill & =P\left(1+\frac{r}{n}\right)^{nt}\hfill & \text{Use the compound interest formula}. \\ A\left(10\right)\hfill & =3000\left(1+\frac{0.03}{4}\right)^{4\cdot 10}\hfill & \text{Substitute using given values}. \\ \text{ }\hfill & \approx 4045.05\hfill & \text{Round to two decimal places}.\end{array}[/latex]

The account will be worth about [latex]$4,045.05[/latex] in [latex]10[/latex] years.

The following video shows an example of using an exponential growth to calculate interest compounded quarterly. https://youtu.be/3az4AKvUmmI In our next example we will use the compound interest formula to solve for the principal.

Example

A [latex]529[/latex] Plan is a college-savings plan that allows relatives to invest money to pay for a child’s future college tuition; the account grows tax-free. Lily wants to set up a [latex]529[/latex] account for her new granddaughter and wants the account to grow to [latex]$40,000[/latex] over [latex]18[/latex] years. She believes the account will earn [latex]6\%[/latex] compounded semi-annually (twice a year). To the nearest dollar, how much will Lily need to invest in the account now?

Answer:

The nominal interest rate is [latex]6\%[/latex], so r = [latex]0.06[/latex]. Interest is compounded twice a year, so  [latex]<em>k </em>= 2[/latex].

We want to find the initial investment, P, needed so that the value of the account will be worth [latex]$40,000[/latex] in [latex]18[/latex] years. Substitute the given values into the compound interest formula, and solve for P.

[latex]\begin{array}{c}A\left(t\right)\hfill & =P{\left(1+\frac{r}{n}\right)}^{nt}\hfill & \text{Use the compound interest formula}.\hfill \\ 40,000\hfill & =P{\left(1+\frac{0.06}{2}\right)}^{2\left(18\right)}\hfill & \text{Substitute using given values }A\text{, }r, n\text{, and }t.\hfill \\ 40,000\hfill & =P{\left(1.03\right)}^{36}\hfill & \text{Simplify}.\hfill \\ \frac{40,000}{{\left(1.03\right)}^{36}}\hfill & =P\hfill & \text{Isolate }P.\hfill \\ P\hfill & \approx 13,801\hfill & \text{Divide and round to the nearest dollar}.\hfill \end{array}[/latex]

Lily will need to invest [latex]$13,801[/latex] to have [latex]$40,000[/latex] in [latex]18[/latex] years.

In the following video we show another example of finding the deposit amount necessary to obtain a future value from compounded interest. https://youtu.be/saq9dF7a4r8

Summary

Exponential growth grows by a rate proportional to the current amount. For any real number x and any positive real numbers a and b such that [latex]b\ne 1[/latex], an exponential growth function has the form [latex]f\left(x\right)=a{b}^{x}[/latex].  Evaluating exponential functions requires careful attention to the order of operations. Compound interest is an example of exponential growth.

Licenses & Attributions

CC licensed content, Original

  • Determine Exponential Function Values and Graph the Function. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Evaluate a Given Exponential Function to Predict a Future Population. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Ex 1: Compounded Interest Formula - Quarterly. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Compounded Interest Formula - Determine Deposit Needed (Present Value). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.