We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Define and Evaluate Roots

Learning Objectives

  • Define and evaluate principal square roots
  • Define and evaluate nth roots
  • Estimate roots that are not perfect
The most common root is the square root. First, we will define what square roots are,  and how you find the square root of a number. Then we will apply similar ideas to define and evaluate nth roots. Roots are the inverse of exponents, much like multiplication is the inverse of division. Recall how exponents are defined, and written; with an exponent, as words, and as repeated multiplication. Exponent: [latex] {{3}^{2}}[/latex], [latex] {{4}^{5}}[/latex], [latex] {{x}^{3}}[/latex], [latex] {{x}^{\text{n}}}[/latex] Name: “Three squared” or “Three to the second power”, “Four to the fifth power”, “x cubed”, “x to the nth power” Repeated Multiplication: [latex] 3\cdot 3[/latex],  [latex] 4\cdot 4\cdot 4\cdot 4\cdot 4[/latex],  [latex] x\cdot x\cdot x[/latex],  [latex] \underbrace{x\cdot x\cdot x...\cdot x}_{n\text{ times}}[/latex]. Conversely,  when you are trying to find the square root of a number (say, [latex]25[/latex]), you are trying to find a number that can be multiplied by itself to create that original number. In the case of [latex]25[/latex], you can find that [latex]5\cdot5=25[/latex], so [latex]5[/latex] must be the square root.

Square Roots

The symbol for the square root is called a radical symbol and looks like this: [latex]\sqrt{\,\,\,}[/latex]. The expression [latex] \sqrt{25}[/latex] is read “the square root of twenty-five” or “radical twenty-five.” The number that is written under the radical symbol is called the radicand.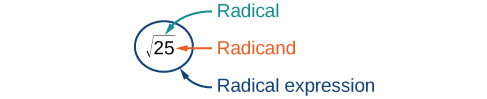 The expression: square root of twenty-five is enclosed in a circle. The circle has an arrow pointing to it labeled: Radical expression. The square root symbol has an arrow pointing to it labeled: Radical. The number twenty-five has an arrow pointing to it labeled: Radicand. The following table shows different radicals and their equivalent written and simplified forms.
Radical Name Simplified Form
[latex] \sqrt{36}[/latex] “Square root of thirty-six” “Radical thirty-six” [latex] \sqrt{36}=\sqrt{6\cdot 6}=6[/latex]
[latex] \sqrt{100}[/latex] “Square root of one hundred” “Radical one hundred” [latex] \sqrt{100}=\sqrt{10\cdot 10}=10[/latex]
[latex] \sqrt{225}[/latex] “Square root of two hundred twenty-five” “Radical two hundred twenty-five” [latex] \sqrt{225}=\sqrt{15\cdot 15}=15[/latex]
Consider [latex] \sqrt{25}[/latex] again. You may realize that there is another value that, when multiplied by itself, also results in [latex]25[/latex]. That number is [latex]−5[/latex].

[latex] \begin{array}{r}5\cdot 5=25\\-5\cdot -5=25\end{array}[/latex]

By definition, the square root symbol always means to find the positive root, called the principal root. So while [latex]5\cdot5[/latex] and [latex]−5\cdot−5[/latex] both equal [latex]25[/latex], only [latex]5[/latex] is the principal root. You should also know that zero is special because it has only one square root: itself (since [latex]0\cdot0=0[/latex]). In our first example we will show you how to use radical notation to evaluate principal square roots.

Example

Find the principal root of each expression.
  1. [latex]\sqrt{100}[/latex]
  2. [latex]\sqrt{16}[/latex]
  3. [latex]\sqrt{25+144}[/latex]
  4. [latex]\sqrt{49}-\sqrt{81}[/latex]
  5. [latex] -\sqrt{81}[/latex]
  6. [latex]\sqrt{-9}[/latex]

Answer:

  1. [latex]\sqrt{100}=10[/latex] because [latex]{10}^{2}=100[/latex]
  2. [latex]\sqrt{16}=4[/latex] because [latex]{4}^{2}=16[/latex]
  3. Recall that square roots act as grouping symbols in the order of operations, so addition and subtraction must be performed first when they occur under a radical. [latex]\sqrt{25+144}=\sqrt{169}=13[/latex] because [latex]{13}^{2}=169[/latex]
  4. This problem is similar to the last one, but this time subtraction should occur after evaluating the root. Stop and think about why these two problems are different. [latex]\sqrt{49}-\sqrt{81}=7 - 9=-2[/latex] because [latex]{7}^{2}=49[/latex] and [latex]{9}^{2}=81[/latex]

  5. The negative in front means to take the opposite of the value after you simplify the radical. [latex] -\sqrt{81}\\-\sqrt{9\cdot 9}[/latex].  The square root of [latex]81[/latex] is [latex]9[/latex]. Then, take the opposite of [latex]9[/latex]. [latex]−(9)[/latex]

  6. [latex]\sqrt{-9}[/latex], we are looking for a number that when it is squared, returns [latex]-9[/latex]. We can try [latex](-3)^2[/latex], but that will give a positive result, and [latex]3^2[/latex] will also give a positive result. This leads to an important fact -  you cannot find the square root of a negative number.

In the following video we present more examples of how to find a principle square root. https://youtu.be/2cWAkmJoaDQ The last example we showed leads to an important characteristic of square roots. You can only take the square root of values that are nonnegative.

Domain of a Square Root [latex]\sqrt{-a}[/latex] is not defined for all real numbers, a. Therefore, [latex]\sqrt{a}[/latex] is defined for [latex]a\ge0[/latex]

Think About It

Does [latex]\sqrt{25}=\pm 5[/latex]? Write your ideas and a sentence to defend them in the box below before you look at the answer. [practice-area rows="1"][/practice-area]

Answer: No. Although both [latex]{5}^{2}[/latex] and [latex]{\left(-5\right)}^{2}[/latex] are [latex]25[/latex], the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is [latex]\sqrt{25}=5[/latex].

Cube Roots

We know that [latex]5^2=25, \text{ and }\sqrt{25}=5[/latex] but what if we want to "undo" [latex]5^3=125, \text{ or }5^4=625[/latex]? We can use higher order roots to answer these questions. Suppose we know that [latex]{a}^{3}=8[/latex]. We want to find what number raised to the [latex]3[/latex]rd power is equal to [latex]8[/latex]. Since [latex]{2}^{3}=8[/latex], we say that [latex]2[/latex] is the cube root of [latex]8[/latex]. In the next example we will evaluate the cube roots of some perfect cubes.

Example

Evaluate the following:
  1. [latex] \sqrt[3]{125}[/latex]
  2. [latex] \sqrt[3]{-8}[/latex]
  3. [latex] \sqrt[3]{27}[/latex]

Answer: 1. You can read this as “the third root of [latex]125[/latex]” or “the cube root of [latex]125[/latex].” To evaluate this expression, look for a number that, when multiplied by itself two times (for a total of three identical factors), equals [latex]125[/latex]. [latex]\text{?}\cdot\text{?}\cdot\text{?}=125[/latex]. Since [latex]125[/latex] ends in [latex]5, 5[/latex] is a good candidate. [latex]5\cdot{5}\cdot{5}=125[/latex] 2. We want to find a number whose cube is [latex]-8[/latex]. We know [latex]2[/latex] is the cube root of [latex]8[/latex], so maybe we can try [latex]-2[/latex]. [latex]-2\cdot{-2}\cdot{-2}=-8[/latex], so the cube root of [latex]-8[/latex] is [latex]-2[/latex]. This is different from square roots because multiplying three negative numbers together results in a negative number 3. We want to find a number whose cube is [latex]27[/latex]. [latex]3\cdot{3}\cdot{3}=27[/latex] the cube root of [latex]27[/latex] is [latex]3[/latex].

As we saw in the last example,there is one interesting fact about cube roots that is not true of square roots. Negative numbers can’t have real number square roots, but negative numbers can have real number cube roots! What is the cube root of [latex]−8[/latex]? [latex] \sqrt[3]{-8}=-2[/latex] because [latex] -2\cdot -2\cdot -2=-8[/latex]. Remember, when you are multiplying an odd number of negative numbers, the result is negative! Consider [latex] \sqrt[3]{{{(-1)}^{3}}}=-1[/latex]. In the following video we show more examples of finding a cube root. https://youtu.be/9Nh-Ggd2VJo

Nth Roots

The cube root of a number is written with a small number [latex]3[/latex], called the index, just outside and above the radical symbol. It looks like [latex] \sqrt[3]{{}}[/latex]. This little [latex]3[/latex] distinguishes cube roots from square roots which are written without a small number outside and above the radical symbol. We can apply the same idea to any exponent and it's corresponding root.  The nth root of [latex]a[/latex] is a number that, when raised to the nth power, gives [latex]a[/latex]. For example, [latex]3[/latex] is the 5th root of [latex]243[/latex] because [latex]{\left(3\right)}^{5}=243[/latex]. If [latex]a[/latex] is a real number with at least one nth root, then the principal nth root of [latex]a[/latex] is the number with the same sign as [latex]a[/latex] that, when raised to the nth power, equals [latex]a[/latex]. The principal nth root of [latex]a[/latex] is written as [latex]\sqrt[n]{a}[/latex], where [latex]n[/latex] is a positive integer greater than or equal to [latex]2[/latex]. In the radical expression, [latex]n[/latex] is called the index of the radical.

Definition: Principal nth Root

If [latex]a[/latex] is a real number with at least one nth root, then the principal nth root of [latex]a[/latex], written as [latex]\sqrt[n]{a}[/latex], is the number with the same sign as [latex]a[/latex] that, when raised to the nth power, equals [latex]a[/latex]. The index of the radical is [latex]n[/latex].

Example

Evaluate each of the following:
  1. [latex]\sqrt[5]{-32}[/latex]
  2. [latex]\sqrt[4]{81}[/latex]
  3. [latex]\sqrt[8]{-1}[/latex]

Answer:

  1. [latex]\sqrt[5]{-32}[/latex] Factor [latex]32[/latex], because [latex]{\left(-2\right)}^{5}=-32 \\ \text{ }[/latex]
  2. [latex]\sqrt[4]{81}[/latex]. Factoring can help, we know that [latex]9\cdot9=81[/latex] and we can further factor each [latex]9[/latex]: [latex]\sqrt[4]{81}=\sqrt[4]{3\cdot3\cdot3\cdot3}=\sqrt[4]{3^4}=3[/latex]
  3. [latex]\sqrt[8]{-1}[/latex], since we have an [latex]8[/latex]th root - which is even- with a negative number as the radicand, this root has no real number solutions. In other words, [latex]-1\cdot-1\cdot-1\cdot-1\cdot-1\cdot-1\cdot-1\cdot-1=+1[/latex]

In the following video we show more examples of how to evaluate and nth root. https://youtu.be/vA2DkcUSRSk You can find the odd root of a negative number, but you cannot find the even root of a negative number. This means you can evaluate the radicals [latex] \sqrt[3]{-81},\ \sqrt[5]{-64}[/latex], and [latex] \sqrt[7]{-2187}[/latex], but you cannot evaluate the radicals [latex] \sqrt[{}]{-100},\ \sqrt[4]{-16}[/latex], or [latex] \sqrt[6]{-2,500}[/latex].

Estimate Roots

An approach to handling roots that are not perfect (squares, cubes, etc.)  is to approximate them by comparing the values to perfect squares, cubes, or nth roots. Suppose you wanted to know the square root of [latex]17[/latex]. Let’s look at how you might approximate it.

Example

Estimate. [latex] \sqrt{17}[/latex]

Answer: Think of two perfect squares that surround [latex]17[/latex]. [latex]17[/latex] is in between the perfect squares [latex]16[/latex] and [latex]25[/latex]. So, [latex] \sqrt{17}[/latex] must be in between [latex] \sqrt{16}[/latex] and [latex] \sqrt{25}[/latex]. Determine whether [latex] \sqrt{17}[/latex] is closer to [latex]4[/latex] or to [latex]5[/latex] and make another estimate.

[latex] \sqrt{16}=4[/latex] and [latex] \sqrt{25}=5[/latex]

Since [latex]17[/latex] is closer to [latex]16[/latex] than [latex]25[/latex], [latex] \sqrt{17}[/latex] is probably about [latex]4.1[/latex] or [latex]4.2[/latex]. Use trial and error to get a better estimate of [latex] \sqrt{17}[/latex]. Try squaring incrementally greater numbers, beginning with [latex]4.1[/latex], to find a good approximation for [latex] \sqrt{17}[/latex].

[latex]\left(4.1\right)^{2}[/latex]

[latex]\left(4.1\right)^{2}[/latex] gives a closer estimate than [latex](4.2)^{2}[/latex].

[latex]4.1\cdot4.1=16.81\\4.2\cdot4.2=17.64[/latex]

Continue to use trial and error to get an even better estimate.

[latex]4.12\cdot4.12=16.9744\\4.13\cdot4.13=17.0569[/latex]

Answer

[latex-display] \sqrt{17}\approx 4.12[/latex-display]

This approximation is pretty close. If you kept using this trial and error strategy you could continue to find the square root to the thousandths, ten-thousandths, and hundred-thousandths places, but eventually it would become too tedious to do by hand. For this reason, when you need to find a more precise approximation of a square root, you should use a calculator. Most calculators have a square root key [latex] (\sqrt{{}})[/latex] that will give you the square root approximation quickly. On a simple [latex]4[/latex]-function calculator, you would likely key in the number that you want to take the square root of and then press the square root key. Try to find [latex] \sqrt{17}[/latex] using your calculator. Note that you will not be able to get an “exact” answer because [latex] \sqrt{17}[/latex] is an irrational number, a number that cannot be expressed as a fraction, and the decimal never terminates or repeats. To nine decimal positions, [latex] \sqrt{17}[/latex] is approximated as [latex]4.123105626[/latex]. A calculator can save a lot of time and yield a more precise square root when you are dealing with numbers that aren’t perfect squares.

Example

Approximate [latex] \sqrt[3]{30}[/latex] and also find its value using a calculator.

Answer: Find the cubes that surround [latex]30[/latex]. [latex]30[/latex] is in between the perfect cubes [latex]27[/latex] and [latex]81[/latex]. [latex] \sqrt[3]{27}=3[/latex] and [latex] \sqrt[3]{81}=4[/latex], so [latex] \sqrt[3]{30}[/latex] is between [latex]3[/latex] and [latex]4[/latex]. Use a calculator.

[latex]\sqrt[3]{30}\approx3.10723[/latex]

Answer

By approximation: [latex]3\ge\sqrt[3]{30}\le4[/latex] Using a calculator: [latex] \sqrt[3]{30}\approx3.10723[/latex]

The following video shows another example of how to estimate a square root. https://youtu.be/iNfalyW7olk

Summary

The square root of a number is the number which, when multiplied by itself, gives the original number. Principal square roots are always positive and the square root of [latex]0[/latex] is [latex]0[/latex]. You can only take the square root of values that are greater than or equal to [latex]0[/latex]. The square root of a perfect square will be an integer. Other roots can be simplified by identifying factors that are perfect squares, cubes, etc. Nth roots can be approximated using trial and error or a calculator.

Licenses & Attributions

CC licensed content, Original

  • Simplify a Variety of Square Expressions (Simplify Perfectly). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Simplify Cube Roots (Perfect Cube Radicands). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Simplify Perfect Nth Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Approximate a Square Root to Two Decimal Places Using Trial and Error. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.

CC licensed content, Shared previously

  • Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • Precalculus. Provided by: Open Stax Authored by: Abramson, Jay. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.