Solutions
Solutions to Try Its
1.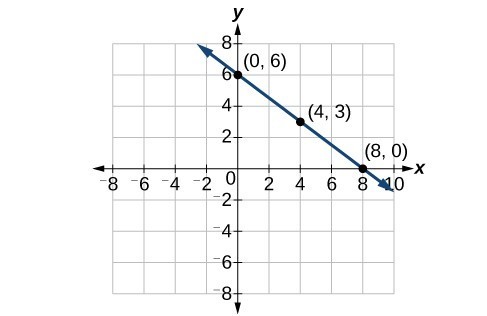 2. Possible answers include [latex]\left(-3,7\right)\\[/latex], [latex]\left(-6,9\right)\\[/latex], or [latex]\left(-9,11\right)\\[/latex].
3.
2. Possible answers include [latex]\left(-3,7\right)\\[/latex], [latex]\left(-6,9\right)\\[/latex], or [latex]\left(-9,11\right)\\[/latex].
3.
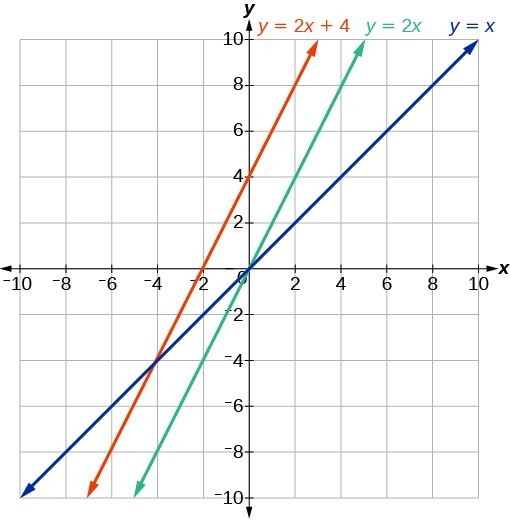 4. [latex]\left(16,\text{ 0}\right)\\[/latex]
5. a. [latex]f\left(x\right)=2x\\[/latex]
b. [latex]g\left(x\right)=-\frac{1}{2}x\\[/latex]
6. [latex]y=-\frac{1}{3}x+6\\[/latex]
7.
4. [latex]\left(16,\text{ 0}\right)\\[/latex]
5. a. [latex]f\left(x\right)=2x\\[/latex]
b. [latex]g\left(x\right)=-\frac{1}{2}x\\[/latex]
6. [latex]y=-\frac{1}{3}x+6\\[/latex]
7.
a. [latex]\left(0,5\right)\\[/latex]
b. [latex]\left(5,\text{ 0}\right)\\[/latex]
c. Slope -1
d. Neither parallel nor perpendicular
e. Decreasing function
f. Given the identity function, perform a vertical flip (over the t-axis) and shift up 5 units.
Solutions to Odd-Numbered Exercises
1. The slopes are equal; y-intercepts are not equal. 3. The point of intersection is [latex]\left(a,a\right)\\[/latex]. This is because for the horizontal line, all of the y coordinates are a and for the vertical line, all of the x coordinates are a. The point of intersection will have these two characteristics. 5. First, find the slope of the linear function. Then take the negative reciprocal of the slope; this is the slope of the perpendicular line. Substitute the slope of the perpendicular line and the coordinate of the given point into the equation [latex]y=mx+b\\[/latex] and solve for b. Then write the equation of the line in the form [latex]y=mx+b\\[/latex] by substituting in m and b. 7. neither parallel or perpendicular 9. perpendicular 11. parallel 13. [latex]\left(-2\text{, }0\right)\\[/latex] ; [latex]\left(0\text{, 4}\right)\\[/latex] 15. [latex]\left(\frac{1}{5}\text{, }0\right)\\[/latex] ; [latex]\left(0\text{, 1}\right)\\[/latex] 17. [latex]\left(8\text{, }0\right)\\[/latex] ; [latex]\left(0\text{, }28\right)\\[/latex] 19. [latex]\text{Line 1}: m=8 \text{ Line 2}: m=-6 \text{Neither}\\[/latex] 21. [latex]\text{Line 1}: m=-\frac{1}{2} \text{ Line 2}: m=2 \text{Perpendicular}\\[/latex] 23. [latex]\text{Line 1}: m=-2 \text{ Line 2}: m=-2 \text{Parallel}\\[/latex] 25. [latex]g\left(x\right)=3x - 3\\[/latex] 27. [latex]p\left(t\right)=-\frac{1}{3}t+2\\[/latex] 29. [latex]\left(-2,1\right)\\[/latex] 31. [latex]\left(-\frac{17}{5},\frac{5}{3}\right)\\[/latex] 33. F 35. C 37. A 39.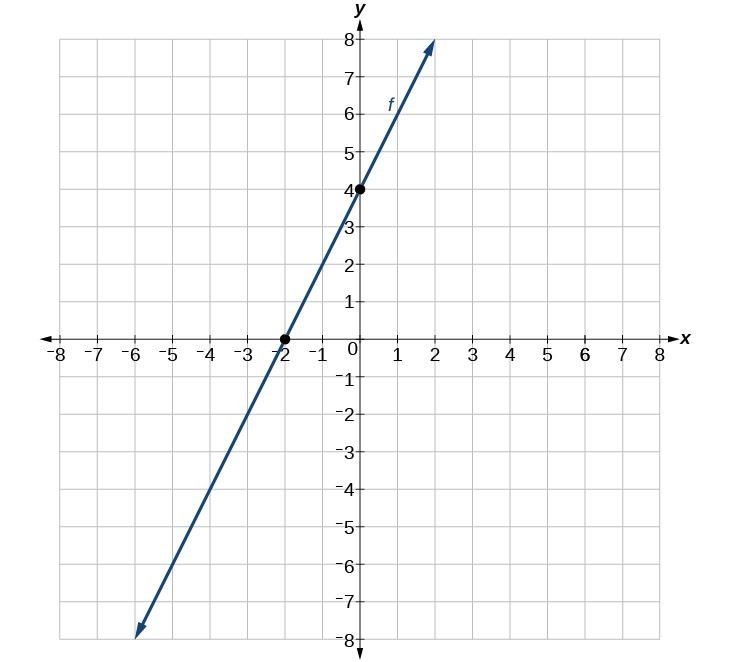 41.
41.
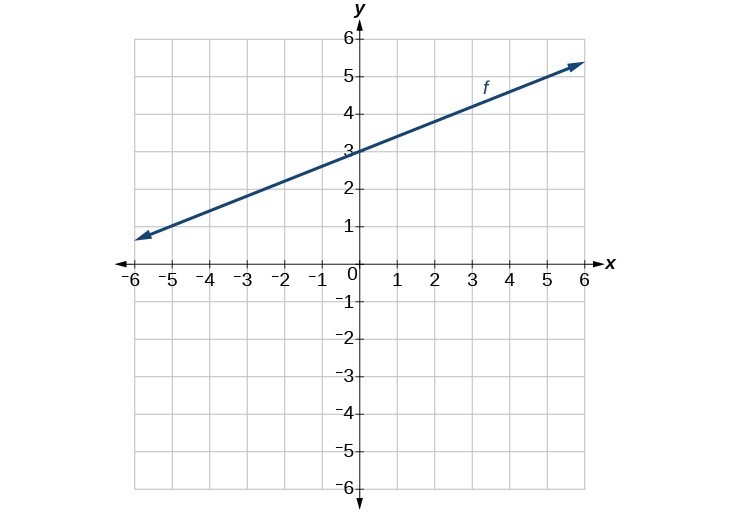 43.
43.
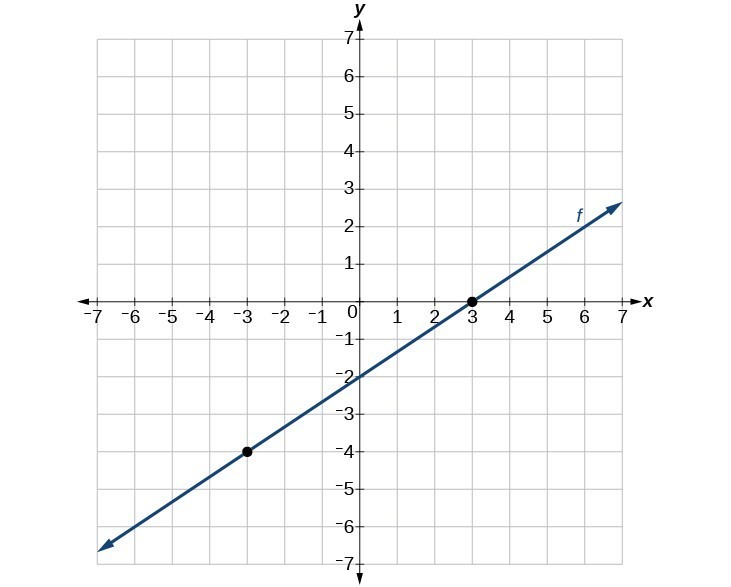 45.
45.
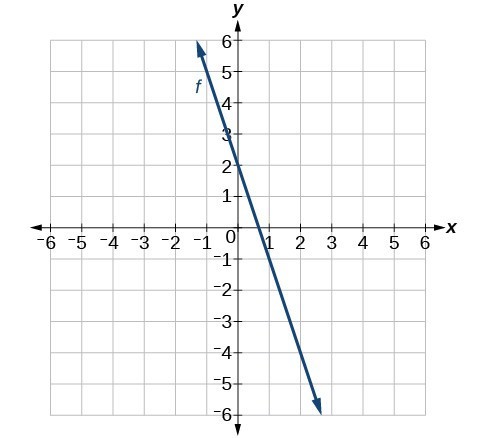 47.
47.
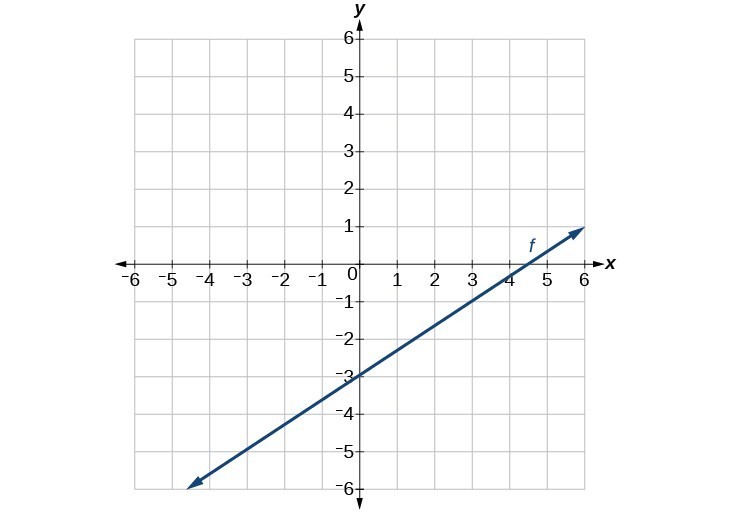 49.
49.
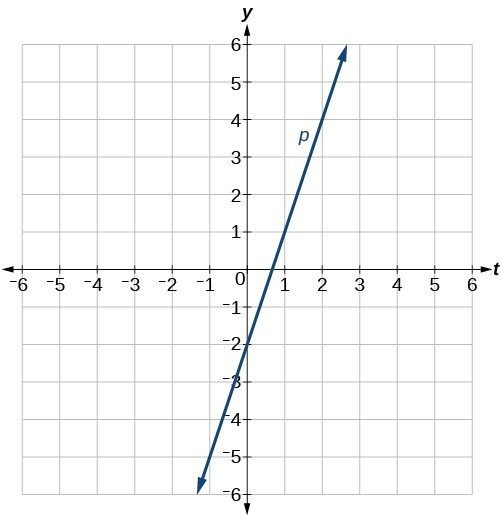 51.
51.
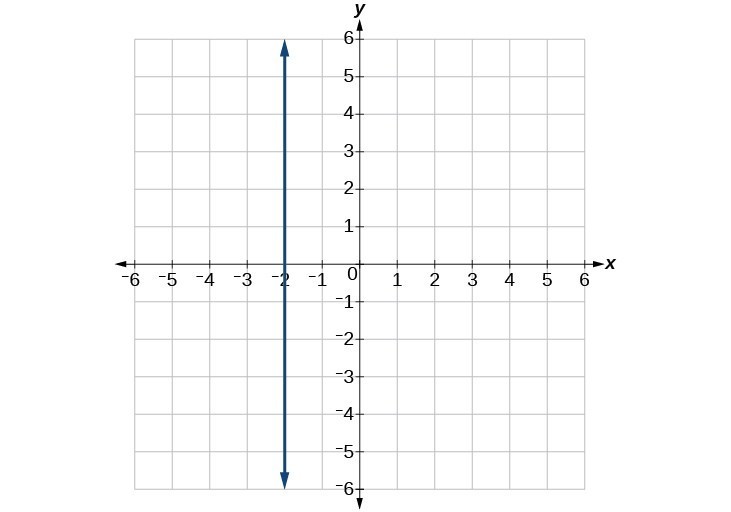 53.
53.
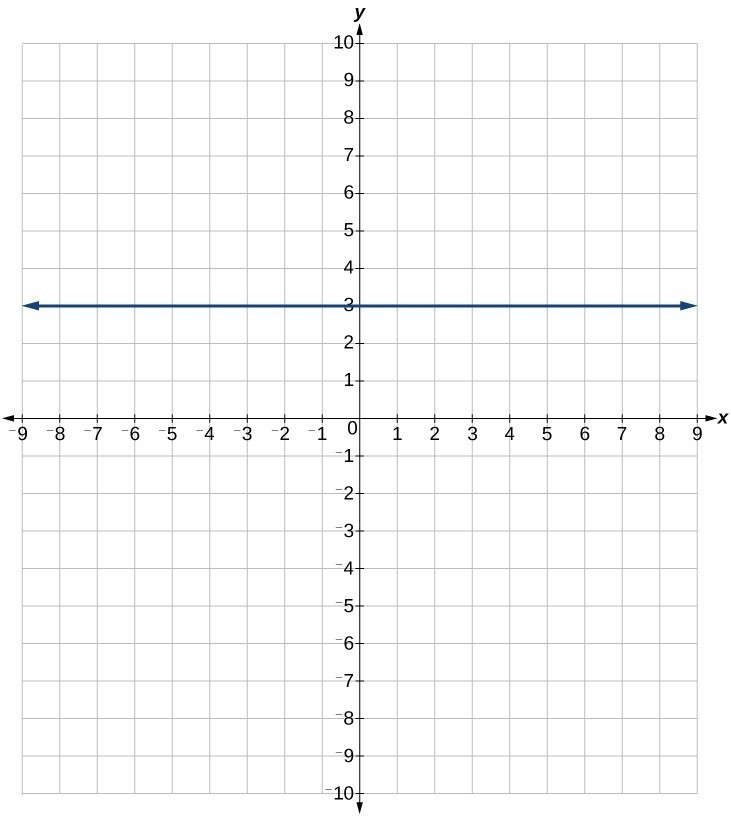 55.
55.
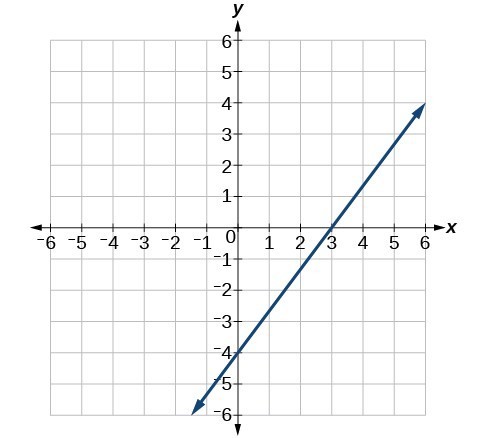 57.
57.
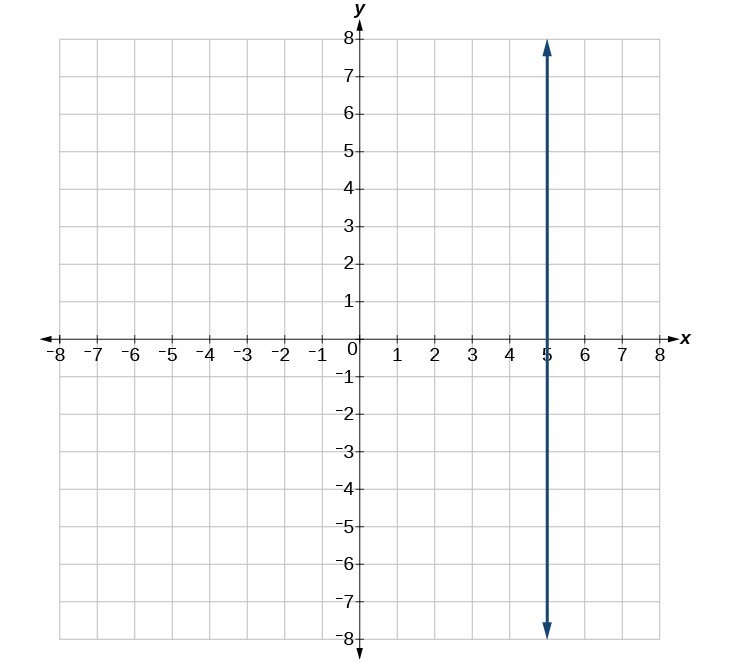 59. [latex]g\left(x\right)=0.75x - 5.5\text{}\\[/latex] 0.75 [latex]\left(0,-5.5\right)\\[/latex]
61. [latex]y=3\\[/latex]
63. [latex]x=-3\\[/latex]
65. no point of intersection
67. [latex]\left(\text{2},\text{ 7}\right)\\[/latex]
69. [latex]\left(-10,\text{ }-5\right)\\[/latex]
71. [latex]y=100x - 98\\[/latex]
73. [latex]x<\frac{1999}{201}x>\frac{1999}{201}\\[/latex]
75. Less than 3000 texts
59. [latex]g\left(x\right)=0.75x - 5.5\text{}\\[/latex] 0.75 [latex]\left(0,-5.5\right)\\[/latex]
61. [latex]y=3\\[/latex]
63. [latex]x=-3\\[/latex]
65. no point of intersection
67. [latex]\left(\text{2},\text{ 7}\right)\\[/latex]
69. [latex]\left(-10,\text{ }-5\right)\\[/latex]
71. [latex]y=100x - 98\\[/latex]
73. [latex]x<\frac{1999}{201}x>\frac{1999}{201}\\[/latex]
75. Less than 3000 texts
Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
