Solutions for Polar Form of Complex Numbers
Solutions to Try Its
1.
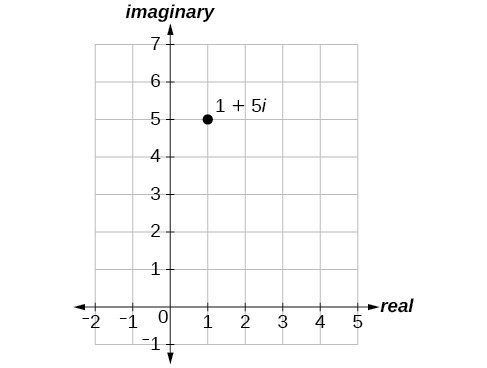2. 13
3. [latex]|z|=\sqrt{50}=5\sqrt{2}[/latex]
4. [latex]z=3\left(\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right)\right)[/latex]
5. [latex]z=2\left(\cos \left(\frac{\pi }{6}\right)+i\sin \left(\frac{\pi }{6}\right)\right)[/latex]
6. [latex]z=2\sqrt{3}-2i[/latex]
7. [latex]{z}_{1}{z}_{2}=-4\sqrt{3};\frac{{z}_{1}}{{z}_{2}}=-\frac{\sqrt{3}}{2}+\frac{3}{2}i[/latex]
8. [latex]{z}_{0}=2\left(\cos \left(30^\circ \right)+i\sin \left(30^\circ \right)\right)[/latex]
[latex-display]{z}_{1}=2\left(\cos \left(120^\circ \right)+i\sin \left(120^\circ \right)\right)[/latex-display]
[latex-display]{z}_{2}=2\left(\cos \left(210^\circ \right)+i\sin \left(210^\circ \right)\right)[/latex-display]
[latex-display]{z}_{3}=2\left(\cos \left(300^\circ \right)+i\sin \left(300^\circ \right)\right)[/latex-display]
Solutions to Odd-Numbered Answers
1. a is the real part, b is the imaginary part, and [latex]i=\sqrt{−1}[/latex] 3. Polar form converts the real and imaginary part of the complex number in polar form using [latex]x=r\cos\theta[/latex] and [latex]y=r\sin\theta[/latex] 5. [latex]z^{n}=r^{n}\left(\cos\left(n\theta\right)+i\sin\left(n\theta\right)\right)[/latex]. It is used to simplify polar form when a number has been raised to a power. 7. [latex]5\sqrt{2}[/latex] 9. [latex]\sqrt{38}[/latex] 11. [latex]\sqrt{14.45}[/latex] 13. [latex]4\sqrt{5}\text{cis}\left(333.4^{\circ}\right)[/latex] 15. [latex]2\text{cis}\left(\frac{\pi}{6}\right)[/latex] 17. [latex]\frac{7\sqrt{3}}{2}+i\frac{7}{2}[/latex] 19. [latex]−2\sqrt{3}−2i[/latex] 21. [latex]−1.5−i\frac{3\sqrt{3}}{2}[/latex] 23. [latex]4\sqrt{3}\text{cis}\left(198^{\circ}\right)[/latex] 25. [latex]\frac{3}{4}\text{cis}\left(180^{\circ}\right)[/latex] 27. [latex]5\sqrt{3}\text{cis}\left(\frac{17\pi}{24}\right)[/latex] 29. [latex]7\text{cis}\left(70^{\circ}\right)[/latex] 31. [latex]5\text{cis}\left(80^{\circ}\right)[/latex] 33. [latex]5\text{cis}\left(\frac{\pi}{3}\right)[/latex] 35. [latex]125\text{cis}\left(135^{\circ}\right)[/latex] 37. [latex]9\text{cis}\left(240^{\circ}\right)[/latex] 39. [latex]\text{cis}\left(\frac{3\pi}{4}\right)[/latex] 41. [latex]3\text{cis}\left(80^{\circ}\right)\text{, }3\text{cis}\left(200^{\circ}\right)\text{, }3\text{cis}\left(320^{\circ}\right)[/latex] 43. [latex]2\sqrt[3]{4}\text{cis}\left(\frac{2\pi}{9}\right)\text{, }2\sqrt[3]{4}\text{cis}\left(\frac{8\pi}{9}\right)\text{, }2\sqrt[3]{4}\text{cis}\left(\frac{14\pi}{9}\right)[/latex] 45. [latex]2\sqrt{2}\text{cis}\left(\frac{7\pi}{8}\right)\text{, }2\sqrt{2}\text{cis}\left(\frac{15\pi}{8}\right)[/latex] 47.
49.
51.
53.
55.
57. [latex]3.61e^{−0.59i}[/latex]
59. [latex]−2+3.46i[/latex]
61. [latex]−4.33−2.50i[/latex]Licenses & Attributions
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
