We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Simplifying Expressions With Different Forms of the Distributive Property

Learning Outcomes

  • Apply the distributive property to simplify an algebraic expression involving whole numbers, integers,  fractions and decimals
  • Apply the distributive property in different forms

Simplify Expressions Using the Distributive Property

Suppose three friends are going to the movies. They each need [latex]$9.25[/latex]; that is, [latex]9[/latex] dollars and [latex]1[/latex] quarter. How much money do they need all together? You can think about the dollars separately from the quarters. The image shows the equation 3 times 9 equal to 27. Below the 3 is an image of three people. Below the 9 is an image of 9 one dollar bills. Below the 27 is an image of three groups of 9 one dollar bills for a total of 27 one dollar bills. The image shows the equation 3 times 25 cents equal to 75 cents. Below the 3 is an image of three people. Below the 25 cents is an image of a quarter. Below the 75 cents is an image of three quarters. They need [latex]3[/latex] times [latex]$9[/latex], so [latex]$27[/latex], and [latex]3[/latex] times [latex]1[/latex] quarter, so [latex]75[/latex] cents. In total, they need [latex]$27.75[/latex]. If you think about doing the math in this way, you are using the Distributive Property.

Distributive Property

If [latex]a,b,c[/latex] are real numbers, then [latex-display]a\left(b+c\right)=ab+ac[/latex-display]

Back to our friends at the movies, we could show the math steps we take to find the total amount of money they need like this: [latex]3(9.25)\\3(9\quad+\quad0.25)\\3(9)\quad+\quad3(0.25)\\27\quad+\quad0.75\\27.75[/latex]

In algebra, we use the Distributive Property to remove parentheses as we simplify expressions. For example, if we are asked to simplify the expression [latex]3\left(x+4\right)[/latex], the order of operations says to work in the parentheses first. But we cannot add [latex]x[/latex] and [latex]4[/latex], since they are not like terms. So we use the Distributive Property, as shown in the next example.

example

Simplify: [latex]3\left(x+4\right)[/latex] Solution:
[latex]3\left(x+4\right)[/latex]
Distribute. [latex]3\cdot x+3\cdot 4[/latex]
Multiply. [latex]3x+12[/latex]
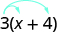Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in the previous example would look like this: The image shows the expression x plus 4 in parentheses with the number 3 outside the parentheses on the left. There are two arrows pointing from the top of the three. One arrow points to the top of the x. The other arrow points to the top of the 4. [latex-display]3\cdot x+3\cdot 4[/latex-display] Now you try.

try it

#146473 [ohm_question]146473[/ohm_question]
In our next example, there is a coefficient on the variable y. When you use the distributive property, you multiply the two numbers together, just like simplifying any product. You will also see another example where the expression in parentheses is subtraction, rather than addition.  You will need to be careful to change the sign of your product.  

example

Simplify: [latex]6\left(5y+1\right)[/latex].

Answer:   Solution:

.
Distribute. [latex]6\cdot 5y+6\cdot 1[/latex]
Multiply. [latex]30y+6[/latex]

Simplify: [latex]2\left(x - 3\right)[/latex]

Answer: Solution:

.
Distribute. [latex]2\cdot x--2\cdot 3[/latex]
Multiply. [latex]2x--6[/latex]

Now you try.

try it

#146474 [ohm_question]146474[/ohm_question] #146475 [ohm_question]146475[/ohm_question]
The distributive property can be used to simplify expressions that look slightly different from [latex]a\left(b+c\right)[/latex]. Here are two other forms.

different Forms of the Distributive Property

If [latex]a,b,c[/latex] are real numbers, then [latex-display]a\left(b+c\right)=ab+ac[/latex-display] Other forms [latex-display]a\left(b-c\right)=ab-ac[/latex-display] [latex-display]\left(b+c\right)a=ba+ca[/latex-display]
In teh following video we show more examples of using the distributive property. https://youtu.be/Nt8V5cEvAz8

Using the Distributive Property With Fractions and Decimals

Do you remember how to multiply a fraction by a whole number? We’ll need to do that in the next two examples. The distributive property comes in all shapes and sizes, and can include fractions or decimals as well.

example

Simplify: [latex]\frac{3}{4}\left(n+12\right)[/latex]

Answer: Solution:

.
Distribute. [latex]\frac{3}{4}\cdot n+\frac{3}{4}\cdot 12[/latex]
Simplify. [latex]\frac{3}{4}n+9[/latex]

Simplify: [latex]8\left(\frac{3}{8}x+\frac{1}{4}\right)[/latex].

Answer: Solution:

.
Distribute. [latex]8\cdot\frac{3}{8}x+8\cdot\frac{1}{4}[/latex]
Multiply. [latex]3x+2[/latex]

Now you try.

try it

[ohm_question]146476[/ohm_question] [ohm_question]146479[/ohm_question]
Using the Distributive Property as shown in the next example will be very useful when we solve money applications later.

example

Simplify: [latex]100\left(0.3+0.25q\right)[/latex]

Answer: Solution:

.
Distribute. [latex]100(0.3)+100(0.25q)[/latex]
Multiply. [latex]30+25q[/latex]

Now you try.

try it

[ohm_question]146505[/ohm_question]

Distributing a Variable

In the next example we’ll multiply by a variable. We’ll need to do this in a later chapter.

example

Simplify: [latex]m\left(n - 4\right)[/latex]

Answer: Solution:

.
Distribute. [latex]m\cdot n--m\cdot n[/latex]
Multiply. [latex]mn--4m[/latex]
Notice that we wrote [latex]m\cdot 4\text{as}4m[/latex]. We can do this because of the Commutative Property of Multiplication. When a term is the product of a number and a variable, we write the number first.

Now you try.

try it

[ohm_question]146506[/ohm_question]

The Backwards Form of the Distributive Property

The next example will use the ‘backwards’ form of the Distributive Property, [latex]\left(b+c\right)a=ba+ca[/latex].

example

Simplify: [latex]\left(x+8\right)p[/latex]

Answer: Solution:

.
Distribute. .

try it

[ohm_question]146507[/ohm_question]

Distributing a Negative Term

When you distribute a negative number, you need to be extra careful to get the signs correct.

example

Simplify: [latex]-2\left(4y+1\right)[/latex]

Answer: Solution:

.
Distribute. [latex]--2\cdot 4y+(--2)\cdot 1[/latex]
Simplify. [latex]--8y--2[/latex]

Simplify: [latex]-11\left(4 - 3a\right)[/latex]

Answer: Solution:

[latex]--11(4--3a)[/latex]
Distribute. [latex]--11\cdot 4--(--11)\cdot 3a[/latex]
Multiply. [latex]--44+(--33a)[/latex]
Simplify. [latex]--44+33a[/latex]
You could also write the result as [latex]33a - 44[/latex]. Do you know why?

try it

[ohm_question]146512[/ohm_question] [ohm_question]146511[/ohm_question]
In the next example, we will show how to use the Distributive Property to find the opposite of an expression. Remember, [latex]-a=-1\cdot a[/latex].

example

Simplify: [latex]-\left(y+5\right)[/latex]

Answer: Solution:

[latex]--(y+5)[/latex]
Multiplying by −1 results in the opposite. [latex]--1(y+5)[/latex]
Distribute. [latex]--1\cdot y+(--1)\cdot 5[/latex]
Simplify. [latex]--y+(--5)[/latex]
Simplify. [latex]--y--5[/latex]

try it

[ohm_question]146513[/ohm_question]

Licenses & Attributions

CC licensed content, Original

  • Question ID 146513, 146511, 146510, 146509, 146506, 146505. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Ex 1: The Distributive Property. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Ex 3: Combining Like Terms Requiring Distribution. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.

CC licensed content, Specific attribution