We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Solve Compound Inequalities—AND

Learning Outcomes

  • Express solutions to inequalities graphically and using interval notation
  • Identify solutions for compound inequalities in the form [latex]a<x<b[/latex] including cases with no solution

Solve Compound Inequalities in the Form of "and" and Express the Solution Graphically

The solution of a compound inequality that consists of two inequalities joined with the word and is the intersection of the solutions of each inequality. In other words, both statements must be true at the same time. The solution to an and compound inequality are all the solutions that the two inequalities have in common. As we saw in previous sections, this is where the two graphs overlap. In this section we will see more examples where we have to simplify the compound inequalities before we can express their solutions graphically or with an interval.

Example

Solve for x. [latex] \displaystyle 1-4x\le 21\,\,\,\,\text{and}\,\,\,\,5x+2\ge22[/latex]

Answer: Solve each inequality for x. Determine the intersection of the solutions.

[latex] \displaystyle \begin{array}{r}\,\,\,1-4x\le 21\,\,\,\,\,\,\,\,\textit{and}\,\,\,\,\,\,\,5x+2\ge 22\\\underline{-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,-2\,\,\,\,-2}\\\,\,\,\,\,\underline{-4x}\leq \underline{20}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{5x}\ge \underline{20}\\\,\,\,\,\,{-4}\,\,\,\,\,\,\,{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,x\ge -5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\ge 4\,\,\,\,\\\\x\ge -5\,\textit{and}\,\,x\ge 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

The number line below shows the graphs of the two inequalities in the problem. The solution to the compound inequality is [latex]x\geq4[/latex] since this is where the two graphs overlap.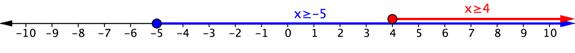 Number line. Closed blue circle on negative 5 and blue arrow through all numbers greater than negative 5. This blue arrow is labeled x is greater than or equal to negative 5. Closed red circle on 4 and red arrow through all numbers greater than 4. This red line is labeled x is greater than or equal to 4. Inequality notation: [latex] \displaystyle x\ge 4[/latex] Interval notation: [latex]\left[4,\infty\right)[/latex] Graph: Number line. Closed purple circle (overlapping red and blue circles) on 4 and purple arrow through all numbers greater than 4. Purple line is labeled x is greater than or equal to 4.

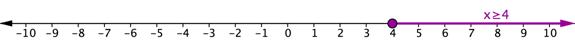
Example

Solve for x:  [latex] \displaystyle {5}{x}-{2}\le{3}\text{ and }{4}{x}{+7}>{3}[/latex]

Answer: Solve each inequality separately. Find the overlap between the solutions.

[latex] \displaystyle \begin{array}{r}\,\,\,5x-2\le 3\,\,\,\,\,\,\,\,\,\textit{and}\,\,\,\,\,\,\,4x+7>\,\,\,\,3\\\underline{\,\,\,\,\,\,\,\,\,\,\,+2\,\,+2\,}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,\,\,\,\,-7\,\,\,\,\,-7}\\\,\,\,\,\underline{5x}\le\underline{\,5\,}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{4x}> \underline{-4}\\\,\,\,\,\,{5}\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,{4}\,\,\\\,\,\,\,\,\,\,\,\,\,\,x\le 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x>-1\,\,\\\\x\le1\,\textit{and}\,\,x>-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Inequality notation: [latex]-1<{x}\le{1}[/latex] Interval notation: [latex](-1,1][/latex] Graph:image

Compound Inequalities in the Form [latex]a<x<b[/latex]

Rather than splitting a compound inequality in the form of  [latex]a<x<b[/latex] into two inequalities [latex]x<b[/latex] and [latex]x>a[/latex], you can more quickly solve the inequality by applying the properties of inequalities to all three segments of the compound inequality.

Example

Solve for x. [latex]3\lt2x+3\leq 7[/latex]

Answer: Isolate the variable by subtracting 3 from all 3 parts of the inequality then dividing each part by 2.

[latex]\begin{array}{r}\,\,\,\,3\,\,\lt\,\,2x+3\,\,\leq \,\,\,\,7\\\underline{\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\underline{\,-3}\\\,\,\,\,\,\underline{\,0\,}\,\,\lt\,\,\,\,\,\,\,\underline{2x}\,\,\,\,\,\leq\,\,\,\underline{\,4\,}\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\\\,\,\,\,\,\,\,\,\,\,0\lt x\leq 2\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Inequality notation: [latex] \displaystyle 0\lt{x}\le 2[/latex] Interval notation: [latex]\left(0,2\right][/latex] Graph: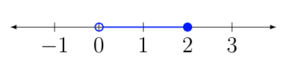 Open dot on zero, closed dot on 2, and line through all numbers between zero and two.

In the video below, you will see another example of how to solve an inequality in the form  [latex]a<x<b[/latex]. https://youtu.be/UU_KJI59_08

Example

Solve the compound inequality with variables in all three parts: [latex]3+x>7x - 2>5x - 10[/latex].

Answer: Let us try the first method: write two inequalities.

[latex]\begin{array}{lll}3+x> 7x - 2\hfill & \textit{and}\hfill & 7x - 2> 5x - 10\hfill \\ 3> 6x - 2\hfill & \hfill & 2x - 2> -10\hfill \\ 5> 6x\hfill & \hfill & 2x> -8\hfill \\ \dfrac{5}{6}> x\hfill & \hfill & x> -4\hfill \\ x< \dfrac{5}{6}\hfill & \hfill & -4< x\hfill \end{array}[/latex]
The solution set is [latex]-4<x<\dfrac{5}{6}[/latex] or in interval notation [latex]\left(-4,\dfrac{5}{6}\normalsize\right)[/latex]. Notice that when we write the solution in interval notation, the smaller number comes first. We read intervals from left to right as they appear on a number line. A number line with the points -4 and 5/6 labeled. Dots appear at these points and a line connects these two dots.

To solve inequalities like [latex]a<x<b[/latex], use the addition and multiplication properties of inequality to solve the inequality for x. Whatever operation you perform on the middle portion of the inequality, you must also perform to each of the outside sections as well. Pay particular attention to division or multiplication by a negative. The solution to a compound inequality with and is always the overlap between the solution to each inequality. There are three possible outcomes for compound inequalities joined by the word and:
Case 1:
Description The solution could be all the values between two endpoints
Inequalities [latex]x\le{1}[/latex] and [latex]x\gt{-1}[/latex], or as a bounded inequality: [latex]{-1}\lt{x}\le{1}[/latex]
Interval [latex]\left(-1,1\right][/latex]
Graphs Number line. Open blue circle on negative 1 and blue arrow through all numbers greater than negative 1. The blue arrow represents x is greater than negative 1. Closed red circle on 1 and red arrow through all numbers less than 1. Red arrow written x is less than or equal to 1.Number line. Open blue circle on negative 1. Closed red circle on 1. Overlapping red and blue lines between negative 1 and 1 that represents negative 1 is less than x is less than or equal to 1.
Case 2:
Description The solution could begin at a point on the number line and extend in one direction.
Inequalities [latex]x\gt3[/latex] and [latex]x\ge4[/latex]
Interval [latex]\left[4,\infty\right)[/latex]
Graphs  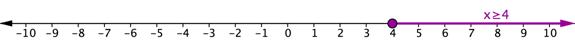Number line. Blue open circle on negative 3 and blue arrow through all numbers greater than negative 3. Blue arrow represents x is greater than negative three. Closed red circle on 4 and red arrow through all numbers greater than 4. The red arrow respresents x is greater than or equal to 4.Number line. Closed circle on 4 and arrow through all numbers greater than 4. The arrow represents x is greater than or equal to 4.
Case 3:
 Description In cases where there is no overlap between the two inequalities, there is no solution to the compound inequality
 Inequalities [latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex]
 Intervals [latex]\left(-\infty,-3\right)[/latex] and [latex]\left(3,\infty\right)[/latex]
 Graph Number line. Open red circle on negative 3 and red arrow through all numbers less than negative 3. Red arrow represents x is less than negative 3. Open blue circle on 3 and blue arrow through all numbers greater than 3. Blue arrow represents x is greater than 3.
In the example below, there is no solution to the compound inequality because there is no overlap between the inequalities.

Example

Solve for x. [latex]x+2>5[/latex] and [latex]x+4<5[/latex]

Answer: Solve each inequality separately.

[latex] \displaystyle \begin{array}{l}x+2>5\,\,\,\,\,\,\,\,\,\textit{and}\,\,\,\,\,\,\,x+4<5\,\,\,\,\\\underline{\,\,\,\,\,-2\,-2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-4\,-4}\\\,\,\,\,\,\,\,\,x>\,\,3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x<\,1\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,x>3\,\,\,\,\textit{and}\,\,\,\,x<1\end{array}[/latex]

Find the overlap between the solutions. Number line. Red open circle is on 1 and red arrow through all numbers less than 1. Red arrow is labeled x is less than 1. Open blue circle on 3 and blue arrow through all numbers greater than 3. Blue arrow represents x is greater than 3. There is no overlap between [latex] \displaystyle x>3[/latex] and [latex]x<1[/latex], so there is no solution.

Summary

A compound inequality is a statement of two inequality statements linked together either by the word or or by the word and. Sometimes, an and compound inequality is shown symbolically, like [latex]a<x<b[/latex] and does not even need the word and. Because compound inequalities represent either a union or intersection of the individual inequalities, graphing them on a number line can be a helpful way to see or check a solution. Compound inequalities can be manipulated and solved in much the same way any inequality is solved, by paying attention to the properties of inequalities and the rules for solving them.

Licenses & Attributions

CC licensed content, Shared previously

  • Ex 1: Solve a Compound Inequality Involving AND (Intersection). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
  • College Algebra. Provided by: OpenStax Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.