Putting it Together: Quadratic Equations and Complex Numbers
 In the beginning of this module, we found Joan and Hazel at the river jumping off a cliff into the water below. Joan recognized the path of their fall as parabolic in shape after seeing a picture Hazel took using continuous mode on her camera while Joan was jumping. They decided to see if they could use physics and math to find out how long they were in the air between the time they jumped and the time they hit the water.
Hazel had found this equation from some old high school physics notes:
In the beginning of this module, we found Joan and Hazel at the river jumping off a cliff into the water below. Joan recognized the path of their fall as parabolic in shape after seeing a picture Hazel took using continuous mode on her camera while Joan was jumping. They decided to see if they could use physics and math to find out how long they were in the air between the time they jumped and the time they hit the water.
Hazel had found this equation from some old high school physics notes:
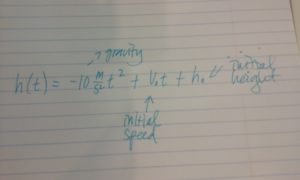
[latex]h(t)=-10\frac{m}{ s^2}t^2+v_{o}t+h_{o}[/latex]
She had labeled the equation with arrows in the following way: [latex]-10\frac{m}{ s^2}[/latex] is gravity, [latex]v_{o}[/latex] is the initial speed of the object, [latex]h_{o}[/latex] is the initial height of the object.
Joan and Hazel decide to define some of the unknowns in the equation. Since they started from a standing position, they decide that [latex]v_{o}=0[/latex]. Then, they estimate that the hight of the cliff was about [latex]15[/latex] meters (or about 45 feet), so [latex]h_{o}=15[/latex]. They use substitution to replace these values in the equation and simplify:
[latex]\begin{array}{c}h(t)=-10\frac{m}{ s^2}{ t^2}+0\cdot{0}\cdot{t}t+15m\\h(t)=-10\frac{m}{ s^2}{ t^2}+15m\end{array}[/latex]
Removing the units: [latex]h(t)=-10{t^2}+15[/latex]
"Now what?" asks Hazel. "I don't remember what we did from here." Joan takes over because she has just finished a module on quadratic equations in her math class, and she knows this is a quadratic equation.
"Our original question was, how long did it take us to fall from the cliff to the water, right? So that means that our height above ground at that time would be equal to zero. I think we should set the equation equal to zero and solve for t."
[latex]h(t)=-10t^{2}+15=0[/latex]
[latex]-10{t}^{2}=-15[/latex]
[latex]{t}^{2}=\frac{3}{2}[/latex]
[latex]\sqrt{ t^2}=\sqrt{\frac{3}{2}}[/latex]
Using a calculator, they evaluate [latex]\sqrt{\frac{3}{2}}[/latex] and get [latex]1.22[/latex].
"Wow! When you are falling it seems longer than [latex]1.22[/latex] seconds!" says Hazel.
Licenses & Attributions
CC licensed content, Shared previously
- Imaginary Numbers Are Real [Part 1: Introduction]. Authored by: Welch Labs. License: All Rights Reserved. License terms: Standard YouTube License.
