Parabolas with Vertices at the Origin
Learning Objectives
- Identify and label the focus, directrix, and endpoints of the focal diameter of a parabola
- Write the equation of a parabola given a focus and directrix
 Parabola
Parabola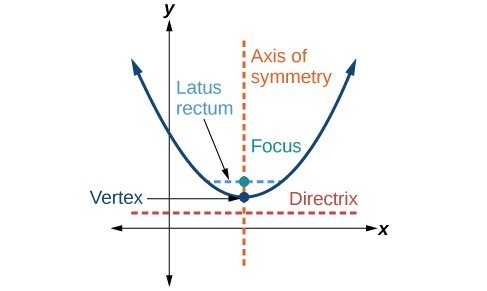 Key features of the parabola
Key features of the parabola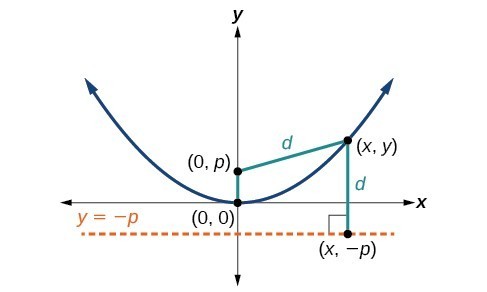 Let [latex]\left(x,y\right)[/latex] be a point on the parabola with vertex [latex]\left(0,0\right)[/latex], focus [latex]\left(0,p\right)[/latex], and directrix [latex]y= -p[/latex] as shown in Figure 4. The distance [latex]d[/latex] from point [latex]\left(x,y\right)[/latex] to point [latex]\left(x,-p\right)[/latex] on the directrix is the difference of the y-values: [latex]d=y+p[/latex]. The distance from the focus [latex]\left(0,p\right)[/latex] to the point [latex]\left(x,y\right)[/latex] is also equal to [latex]d[/latex] and can be expressed using the distance formula.
Let [latex]\left(x,y\right)[/latex] be a point on the parabola with vertex [latex]\left(0,0\right)[/latex], focus [latex]\left(0,p\right)[/latex], and directrix [latex]y= -p[/latex] as shown in Figure 4. The distance [latex]d[/latex] from point [latex]\left(x,y\right)[/latex] to point [latex]\left(x,-p\right)[/latex] on the directrix is the difference of the y-values: [latex]d=y+p[/latex]. The distance from the focus [latex]\left(0,p\right)[/latex] to the point [latex]\left(x,y\right)[/latex] is also equal to [latex]d[/latex] and can be expressed using the distance formula.
[latex]\begin{array}{l}d=\sqrt{{\left(x - 0\right)}^{2}+{\left(y-p\right)}^{2}}\hfill \\ =\sqrt{{x}^{2}+{\left(y-p\right)}^{2}}\hfill \end{array}[/latex]
Set the two expressions for [latex]d[/latex] equal to each other and solve for [latex]y[/latex] to derive the equation of the parabola. We do this because the distance from [latex]\left(x,y\right)[/latex] to [latex]\left(0,p\right)[/latex] equals the distance from [latex]\left(x,y\right)[/latex] to [latex]\left(x, -p\right)[/latex]. [latex-display]\sqrt{{x}^{2}+{\left(y-p\right)}^{2}}=y+p[/latex-display] We then square both sides of the equation, expand the squared terms, and simplify by combining like terms.[latex]\begin{array}{c}{x}^{2}+{\left(y-p\right)}^{2}={\left(y+p\right)}^{2}\\ {x}^{2}+{y}^{2}-2py+{p}^{2}={y}^{2}+2py+{p}^{2}\\ {x}^{2}-2py=2py\\ \text{ }{x}^{2}=4py\end{array}[/latex]
The equations of parabolas with vertex [latex]\left(0,0\right)[/latex] are [latex]{y}^{2}=4px[/latex] when the x-axis is the axis of symmetry and [latex]{x}^{2}=4py[/latex] when the y-axis is the axis of symmetry. These standard forms are given below, along with their general graphs and key features.A General Note: Standard Forms of Parabolas with Vertex (0, 0)
The table below summarizes the standard features of parabolas with a vertex at the origin.| Axis of Symmetry | Equation | Focus | Directrix | Endpoints of Focal Diameter |
| x-axis | [latex]{y}^{2}=4px[/latex] | [latex]\left(p,\text{ }0\right)[/latex] | [latex]x=-p[/latex] | [latex]\left(p,\text{ }\pm 2p\right)[/latex] |
| y-axis | [latex]{x}^{2}=4py[/latex] | [latex]\left(0,\text{ }p\right)[/latex] | [latex]y=-p[/latex] | [latex]\left(\pm 2p,\text{ }p\right)[/latex] |
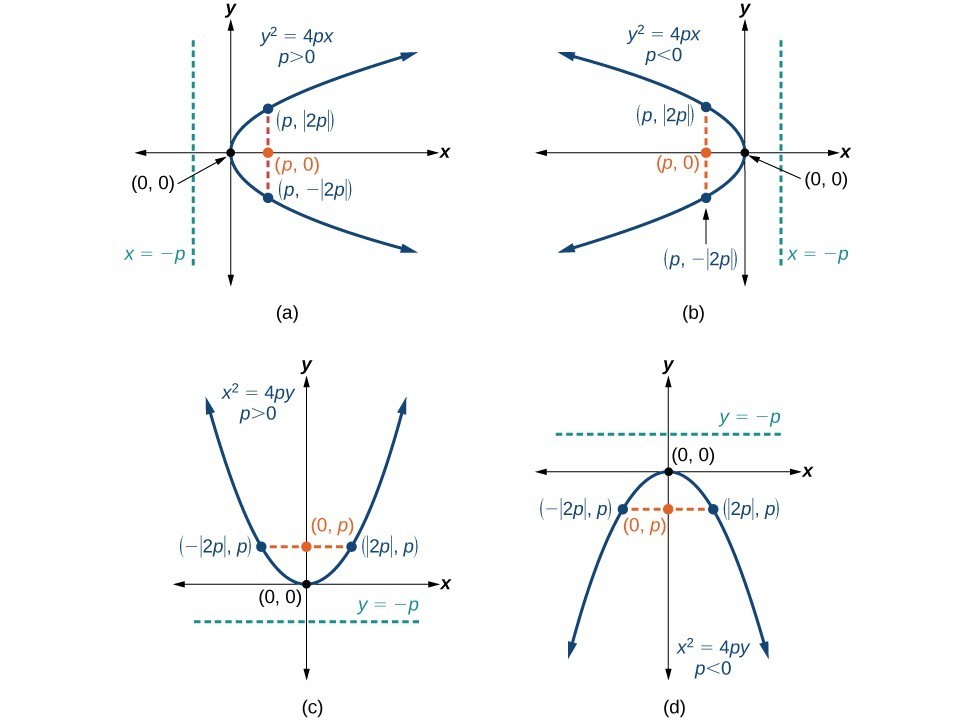 (a) When [latex]p>0[/latex] and the axis of symmetry is the x-axis, the parabola opens right. (b) When [latex]p<0[/latex] and the axis of symmetry is the x-axis, the parabola opens left. (c) When [latex]p<0[/latex] and the axis of symmetry is the y-axis, the parabola opens up. (d) When [latex]\text{ }p<0\text{ }[/latex] and the axis of symmetry is the y-axis, the parabola opens down.
(a) When [latex]p>0[/latex] and the axis of symmetry is the x-axis, the parabola opens right. (b) When [latex]p<0[/latex] and the axis of symmetry is the x-axis, the parabola opens left. (c) When [latex]p<0[/latex] and the axis of symmetry is the y-axis, the parabola opens up. (d) When [latex]\text{ }p<0\text{ }[/latex] and the axis of symmetry is the y-axis, the parabola opens down.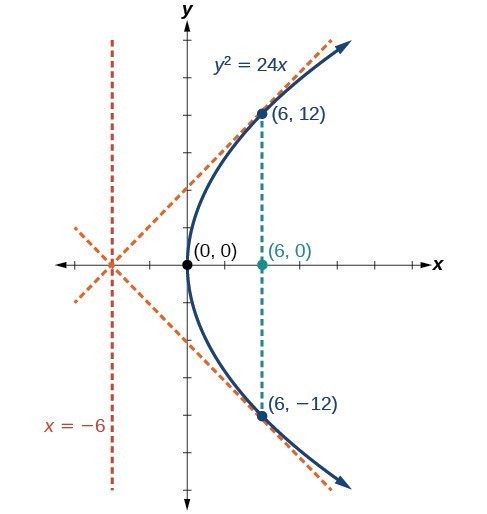
How To: Given a standard form equation for a parabola centered at (0, 0), sketch the graph.
- Determine which of the standard forms applies to the given equation: [latex]{y}^{2}=4px[/latex] or [latex]{x}^{2}=4py[/latex].
- Use the standard form identified in Step 1 to determine the axis of symmetry, focus, equation of the directrix, and endpoints of the focal diameter.
- If the equation is in the form [latex]{y}^{2}=4px[/latex], then
- the axis of symmetry is the x-axis, [latex]y=0[/latex]
- set [latex]4p[/latex] equal to the coefficient of x in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens right. If [latex]p<0[/latex], the parabola opens left.
- use [latex]p[/latex] to find the coordinates of the focus, [latex]\left(p,0\right)[/latex]
- use [latex]p[/latex] to find the equation of the directrix, [latex]x=-p[/latex]
- use [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(p,\pm 2p\right)[/latex]. Alternately, substitute [latex]x=p[/latex] into the original equation.
- If the equation is in the form [latex]{x}^{2}=4py[/latex], then
- the axis of symmetry is the y-axis, [latex]x=0[/latex]
- set [latex]4p[/latex] equal to the coefficient of y in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens up. If [latex]p<0[/latex], the parabola opens down.
- use [latex]p[/latex] to find the coordinates of the focus, [latex]\left(0,p\right)[/latex]
- use [latex]p[/latex] to find equation of the directrix, [latex]y=-p[/latex]
- use [latex]p[/latex] to find the endpoints of the focal diameter, [latex]\left(\pm 2p,p\right)[/latex]
- If the equation is in the form [latex]{y}^{2}=4px[/latex], then
- Plot the focus, directrix, and focal diameter, and draw a smooth curve to form the parabola.
Example: Graphing a Parabola with Vertex (0, 0) and the x-axis as the Axis of Symmetry
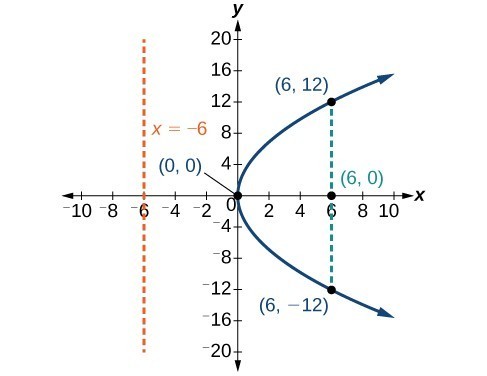
Graph [latex]{y}^{2}=24x[/latex]. Identify and label the focus, directrix, and endpoints of the focal diameter.Answer: The standard form that applies to the given equation is [latex]{y}^{2}=4px[/latex]. Thus, the axis of symmetry is the x-axis. It follows that:
- [latex]24=4p[/latex], so [latex]p=6[/latex]. Since [latex]p>0[/latex], the parabola opens right the coordinates of the focus are [latex]\left(p,0\right)=\left(6,0\right)[/latex]
- the equation of the directrix is [latex]x=-p=-6[/latex]
- the endpoints of the focal diameter have the same x-coordinate at the focus. To find the endpoints, substitute [latex]x=6[/latex] into the original equation: [latex]\left(6,\pm 12\right)[/latex]
Try It
Graph [latex]{y}^{2}=-16x[/latex]. Identify and label the focus, directrix, and endpoints of the focal diameter.Answer:
Focus: [latex]\left(-4,0\right)[/latex]; Directrix: [latex]x=4[/latex]; Endpoints of the latus rectum: [latex]\left(-4,\pm 8\right)[/latex]

Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
- Graphing Parabolas Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/wunbnybenw. License: Public Domain: No Known Copyright.
- Graphing Parabolas - With Solutions Interactive. Authored by: Lumen Learning. Located at: https://www.desmos.com/calculator/b3buagwzwl. License: Public Domain: No Known Copyright.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 23511. Authored by: Shahbazian,Roy, mb McClure,Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 23711. Authored by: McClure,Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
