Finding the Volume and Surface Area of Rectangular Solids

Learning Outcomes

Find the volume and surface area of rectangular solids

A cheerleading coach is having the squad paint wooden crates with the school colors to stand on at the games. (See the image below). The amount of paint needed to cover the outside of each box is the surface area, a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure. This wooden crate is in the shape of a rectangular solid. This is an image of a wooden crate.

Each crate is in the shape of a rectangular solid. Its dimensions are the length, width, and height. The rectangular solid shown in the image below has length [latex]4[/latex] units, width [latex]2[/latex] units, and height [latex]3[/latex] units. Can you tell how many cubic units there are altogether? Let’s look layer by layer. Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This [latex]4[/latex] by [latex]2[/latex] by [latex]3[/latex] rectangular solid has [latex]24[/latex] cubic units. A rectangular solid is shown. Each layer is composed of 8 cubes, measuring 2 by 4. The top layer is pink. The middle layer is orange. The bottom layer is green. Beside this is an image of the top layer that says

A rectangular solid is shown. Each layer is composed of 8 cubes, measuring 2 by 4. The top layer is pink. The middle layer is orange. The bottom layer is green. Beside this is an image of the top layer that says

Altogether there are [latex]24[/latex] cubic units. Notice that [latex]24[/latex] is the [latex]\text{length}\times \text{width}\times \text{height}\text{.}[/latex] The top line says V equals L times W times H. Beneath the V is 24, beneath the equal sign is another equal sign, beneath the L is a 4, beneath the W is a 2, beneath the H is a 3.

The top line says V equals L times W times H. Beneath the V is 24, beneath the equal sign is another equal sign, beneath the L is a 4, beneath the W is a 2, beneath the H is a 3.

The volume, [latex]V[/latex], of any rectangular solid is the product of the length, width, and height. [latex-display]V=LWH[/latex-display] We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, [latex]B[/latex], is equal to [latex]\text{length}\times \text{width}\text{.}[/latex] [latex-display]B=L\cdot W[/latex-display] We can substitute [latex]B[/latex] for [latex]L\cdot W[/latex] in the volume formula to get another form of the volume formula. The top line says V equals red L times red W times H. Below this is V equals red parentheses L times W times H. Below this is V equals red capital B times h.

The top line says V equals red L times red W times H. Below this is V equals red parentheses L times W times H. Below this is V equals red capital B times h.

We now have another version of the volume formula for rectangular solids. Let’s see how this works with the [latex]4\times 2\times 3[/latex] rectangular solid we started with. See the image below. An image of a rectangular solid is shown. It is made up of cubes. It is labeled as 2 by 4 by 3. Beside the solid is V equals Bh. Below this is V equals Base times height. Below Base is parentheses 4 times 2. The next line says V equals parentheses 4 times 2 times 3. Below that is V equals 8 times 3, then V equals 24 cubic units.

An image of a rectangular solid is shown. It is made up of cubes. It is labeled as 2 by 4 by 3. Beside the solid is V equals Bh. Below this is V equals Base times height. Below Base is parentheses 4 times 2. The next line says V equals parentheses 4 times 2 times 3. Below that is V equals 8 times 3, then V equals 24 cubic units.

To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them. [latex-display]\begin{array}{ccccccc}{A}_{\text{front}}=L\times W\hfill & & & {A}_{\text{side}}=L\times W\hfill & & & {A}_{\text{top}}=L\times W\hfill \\ {A}_{\text{front}}=4\cdot 3\hfill & & & {A}_{\text{side}}=2\cdot 3\hfill & & & {A}_{\text{top}}=4\cdot 2\hfill \\ {A}_{\text{front}}=12\hfill & & & {A}_{\text{side}}=6\hfill & & & {A}_{\text{top}}=8\hfill \end{array}[/latex-display] Notice for each of the three faces you see, there is an identical opposite face that does not show. [latex-display]\begin{array}{l}S=\left(\text{front}+\text{back}\right)\text{+}\left(\text{left side}+\text{right side}\right)+\left(\text{top}+\text{bottom}\right)\\ S=\left(2\cdot \text{front}\right)+\left(\text{2}\cdot \text{left side}\right)+\left(\text{2}\cdot \text{top}\right)\\ S=2\cdot 12+2\cdot 6+2\cdot 8\\ S=24+12+16\\ S=52\text{sq. units}\end{array}[/latex-display] The surface area [latex]S[/latex] of the rectangular solid shown above is [latex]52[/latex] square units. In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see the image below). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side. [latex-display]S=2LH+2LW+2WH[/latex-display] For each face of the rectangular solid facing you, there is another face on the opposite side. There are [latex]6[/latex] faces in all. A rectangular solid is shown. The sides are labeled L, W, and H. One face is labeled LW and another is labeled WH.

A rectangular solid is shown. The sides are labeled L, W, and H. One face is labeled LW and another is labeled WH.

Volume and Surface Area of a Rectangular Solid

For a rectangular solid with length [latex]L[/latex], width [latex]W[/latex], and height [latex]H:[/latex] A rectangular solid is shown. The sides are labeled L, W, and H. Beside it is Volume: V equals LWH equals BH. Below that is Surface Area: S equals 2LH plus 2LW plus 2WH.

A rectangular solid is shown. The sides are labeled L, W, and H. Beside it is Volume: V equals LWH equals BH. Below that is Surface Area: S equals 2LH plus 2LW plus 2WH.

Doing the Manipulative Mathematics activity "Painted Cube" will help you develop a better understanding of volume and surface area.

example

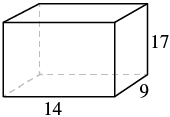
For a rectangular solid with length [latex]14[/latex] cm, height [latex]17[/latex] cm, and width [latex]9[/latex] cm, find 1. the volume and 2. the surface area. Solution Step 1 is the same for both 1. and 2., so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.

1.
Step 2. Identify what you are looking for.	The volume of the rectangular solid
Step 3. Name. Choose a variable to represent it.	Let [latex]V[/latex] = volume
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]V=LWH[/latex] [latex]V=\mathrm{14}cm\cdot 9cm\cdot 17cm[/latex]
Step 5. Solve the equation.	[latex]V=2,142cm^3[/latex]
Step 6. Check We leave it to you to check your calculations.
Step 7. Answer the question.	The volume is [latex]\text{2,142}[/latex] cubic centimeters.

2.
Step 2. Identify what you are looking for.	the surface area of the solid
Step 3. Name. Choose a variable to represent it.	Let [latex]S[/latex] = surface area
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]S=2LH+2LW+2WH[/latex] [latex]S=2\left(14cm\cdot 17cm\right)+2\left(14cm\cdot 9cm\right)+2\left(9cm\cdot 17cm\right)[/latex]
Step 5. Solve the equation.	[latex]S=1,034cm^2[/latex]
Step 6. Check: Double-check with a calculator.
Step 7. Answer the question.	The surface area is [latex]1,034[/latex] square centimeters.

try it

[ohm_question]146790[/ohm_question]

example

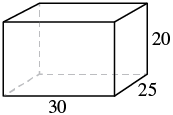
A rectangular crate has a length of [latex]30[/latex] inches, width of [latex]25[/latex] inches, and height of [latex]20[/latex] inches. Find 1. its volume and 2. its surface area.

Answer: Solution Step 1 is the same for both 1. and 2., so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.

1.
Step 2. Identify what you are looking for.	The volume of the crate
Step 3. Name. Choose a variable to represent it.	Let [latex]V[/latex] = volume
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]V=LWH[/latex] [latex]V=30in\cdot 25in\cdot 20in[/latex]
Step 5. Solve the equation.	[latex]V=15,000in^3[/latex]
Step 6. Check: Double check your math.
Step 7. Answer the question.	The volume is [latex]15,000[/latex] cubic inches.

2.
Step 2. Identify what you are looking for.	The surface area of the crate
Step 3. Name. Choose a variable to represent it.	Let [latex]S[/latex] = surface area
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]S=2LH+2LW+2WH[/latex] [latex]S=2\left(30in\cdot 20in\right)+2\left(30in\cdot 25in\right)+2\left(25in\cdot 20in\right)[/latex]
Step 5. Solve the equation.	[latex]S=3,700in^2[/latex]
Step 6. Check: Check it yourself!
Step 7. Answer the question.	The surface area is [latex]3,700[/latex] square inches.

try it

[ohm_question]146789[/ohm_question]

Volume and Surface Area of a Cube

A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get: [latex-display]\begin{array}{ccccc}V=LWH\hfill & & & & S=2LH+2LW+2WH\hfill \\ V=s\cdot s\cdot s\hfill & & & & S=2s\cdot s+2s\cdot s+2s\cdot s\hfill \\ V={s}^{3}\hfill & & & & S=2{s}^{2}+2{s}^{2}+2{s}^{2}\hfill \\ & & & & S=6{s}^{2}\hfill \end{array}[/latex-display] So for a cube, the formulas for volume and surface area are [latex]V={s}^{3}[/latex] and [latex]S=6{s}^{2}[/latex].

Volume and Surface Area of a Cube

For any cube with sides of length [latex]s[/latex], An image of a cube is shown. Each side is labeled s. Beside this is Volume: V equals s cubed. Below that is Surface Area: S equals 6 times s squared.

An image of a cube is shown. Each side is labeled s. Beside this is Volume: V equals s cubed. Below that is Surface Area: S equals 6 times s squared.

example

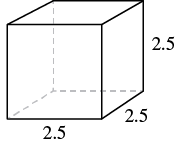
A cube is [latex]2.5[/latex] inches on each side. Find 1. its volume and 2. its surface area. Solution Step 1 is the same for both 1. and 2., so we will show it just once.

Step 1. Read the problem. Draw the figure and label it with the given information.

1.
Step 2. Identify what you are looking for.	The volume of the cube
Step 3. Name. Choose a variable to represent it.	Let V = volume
Step 4. Translate. Write the appropriate formula.	[latex]V={s}^{3}[/latex]
Step 5. Solve. Substitute and solve.	[latex]V={\left(2.5in\right)}^{3}[/latex] [latex]V=15.625in^3[/latex]
Step 6. Check: Check your work.
Step 7. Answer the question.	The volume is [latex]15.625[/latex] cubic inches.

2.
Step 2. Identify what you are looking for.	The surface area of the cube
Step 3. Name. Choose a variable to represent it.	Let S = surface area
Step 4. Translate. Write the appropriate formula.	[latex]S=6{s}^{2}[/latex]
Step 5. Solve. Substitute and solve.	[latex]S=6\cdot {\left(2.5in\right)}^{2}[/latex] [latex]S=37.5in^2[/latex]
Step 6. Check: The check is left to you.
Step 7. Answer the question.	The surface area is [latex]37.5[/latex] square inches.

try it

[ohm_question]146791[/ohm_question]

example

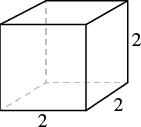
A notepad cube measures [latex]2[/latex] inches on each side. Find 1. its volume and 2. its surface area.

Answer: Solution

Step 1. Read the problem. Draw the figure and label it with the given information.

1.
Step 2. Identify what you are looking for.	The volume of the cube
Step 3. Name. Choose a variable to represent it.	Let V = volume
Step 4. Translate. Write the appropriate formula.	[latex]V={s}^{3}[/latex]
Step 5. Solve the equation.	[latex]V=({2in})^{3}[/latex] [latex]V=8in^3[/latex]
Step 6. Check: Check that you did the calculations correctly.
Step 7. Answer the question.	The volume is [latex]8[/latex] cubic inches.

2.
Step 2. Identify what you are looking for.	The surface area of the cube
Step 3. Name. Choose a variable to represent it.	Let S = surface area
Step 4. Translate. Write the appropriate formula.	[latex]S=6{s}^{2}[/latex]
Step 5. Solve the equation.	[latex]S=6\cdot ({2in})^{2}[/latex] [latex]S=24 in^2[/latex]
Step 6. Check: The check is left to you.
Step 7. Answer the question.	The surface area is [latex]24[/latex] square inches.

try it

[ohm_question]146795[/ohm_question]

Contribute!

Did you have an idea for improving this content? We’d love your input.

Licenses & Attributions

CC licensed content, Original

Question ID 146790, 146789. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Specific attribution

Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].

Study Guides > ALGEBRA / TRIG I

Finding the Volume and Surface Area of Rectangular Solids

Learning Outcomes

Volume and Surface Area of a Rectangular Solid

example

try it

example

try it

Volume and Surface Area of a Cube

Volume and Surface Area of a Cube

example

try it

example

try it

Contribute!

Licenses & Attributions

CC licensed content, Original

CC licensed content, Specific attribution