We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Math for Liberal Arts: Co-requisite Course

Why It Matters: Growth Models

The following essay is adapted from blog posts on emergent math by Geoff Krall.

Can You Predict How Many Followers @charliesheen Has Right Now?

Sometime on March 1, 2011, Charlie Sheen joined twitter at the suggestion of Piers Morgan, who is apparently some type of person. By the time I was alerted of the existence of a @charliesheen twitter feed, it was 4:04 PM Mountain Standard Time. Sheen had yet to tweet, but already had somehow amassed over 100,000 followers. He hadn’t even put up an avatar of himself yet (and somehow the account was “verified”).Screen shot of Charlie Sheen's Twitter page. It shows a blank profile picture, 0 Tweets, 0 Following, 112,497 followers, and 843 Listed. What happened over the next several hours was nothing short of amazing. All you had to do was wait a few seconds or minutes and hit "refresh," and just watch the number of followers climb. I did this for about 50 minutes and collected data along the way.
Time on March 1, 2011 # of Followers
4:04 PM 109,099
4:07 PM 112,497
4:09 PM 116,143
4:12 PM 120,195
4:14 PM 122,901
4:18 PM 127,643
4:21 PM 129,793
4:24 PM 133,357
4:29 PM 140,215
4:32 PM 144,103
4:38 PM 149,528
4:44 PM 153,848
Later that night, I refreshed every half-hour or so and watched the number climbing steadily. At this point, he had made his first tweet. Screen shot of Charlie Sheen's Twitter page. He has a profile picture, and a description under his Twitter handle (@charliesheen) of
Time on March 1, 2011 # of Followers
6:21 PM 261,894
6:24 PM 275,638
6:49 PM 302,077
7:13 PM 324,595
7:38 PM 348,955
8:45 PM 429,904
Eventually I had to go to bed. So I did. And as soon as I woke up the next morning I went back to check Charlie Sheen’s number of twitter followers. Now I’d be checking every hour or so. Recorded here.
Time on March 2, 2011 # of Followers
6:45 AM 729,703
8:51 AM 799,008
9:36 AM 820,538
10:23 AM 841,940
11:16 AM 865,972
12:43 PM 902,291
1:47 PM 926,557
3:09 PM 957,259
The last datum I recorded was at 3:09 MST, at which point @charliesheen had 957,259 followers. So in less than 24 hours, Charlie Sheen had gained 800,000 followers on twitter. I have two questions for you:
  • At what time March, 1, did Charlie Sheen join twitter? and,
  • How many followers does he have right now?
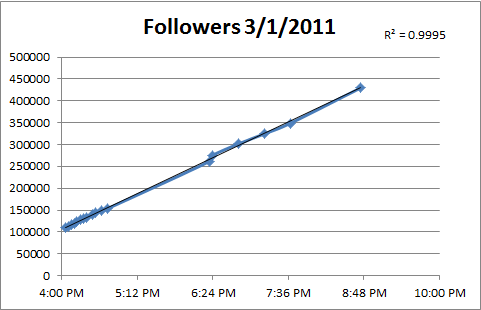To answer, I’ll break this up into a few different time pieces. Here’s the plot of Charlie Sheen’s followers as I have them, only for 3/1/2011, the day he joined twitter. Graph titled “Followers 3/1/2011 R2 = 0.9995) Vertical measures number of followers, in increments of 50,000, from 0 to 500,000. Horizontal measures time, in staggered increments from 4:00PM to 10:00 PM. The plotted points show a straight line moving up to the right, from ~100,000 at 4:00PM to almost 450,000 at 8:49PM. Not only is that a linear fit, it’s very linear (R-squared of 0.9995). I’m also shocked at how straight that line is. That is, there are not spikes of activity. I would have thought that in the evening, when everyone’s sitting in front of their TVs with their iPad 2’s there would be a marked increase in @charliesheen twitter followers. 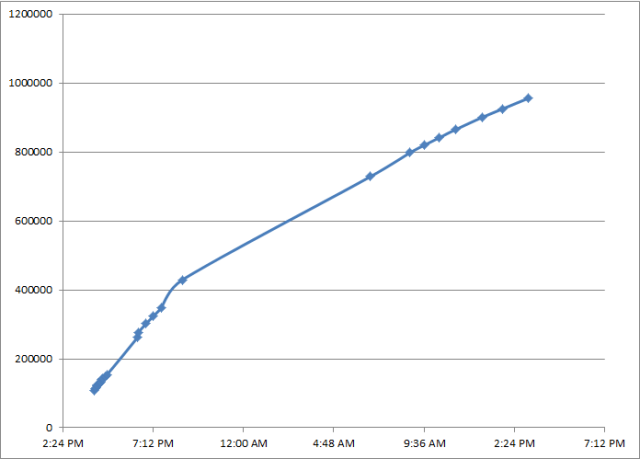Now let’s look at the same graph, but with all of Day 2 (3/2/2011) data included.Graph. Vertical measures number of followers, in increments of 200,000, from 0 to 1,200,000. Horizontal measures time, in staggered increments from 2:24PM to 7:12PM. The plotted points show an initially straight line starting to curve and slow rate of increase, reaching ~900,000 at 2:24PM. Unfortunately, I didn’t check Sheen’s twitter followers in the middle of the night, but it appears to have leveled off slightly going into Day 2 of the twitter account. Now, I’m not 100% sure when the twitter feed account went live – in fact, that was one of the questions I asked last time – but I do have this: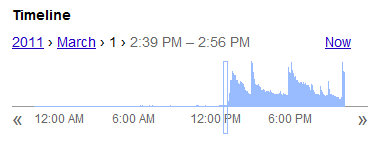Timeline titled “2011 > March > 1 > 2:39PM - 2:56PM” with a link to Now at the top right. It shows no activity starting at 12:00AM, with small lines at 6:00AM staggered far apart. By 12:00PM the lines start to become more frequent, starting small and building quickly in jagged bursts until well after 6:00pm. This is the Google realtime search feature. I would assume there’s a strong correlation between the Google realtime searches for “@charliesheen” and the activation of the twitter account. So it looks like the account may have gone active sometime in the mid-afternoon of 3/1/2011. Let’s call it 3:00 PM. I took a couple of additional data points in the next couple of days, which leads me here: 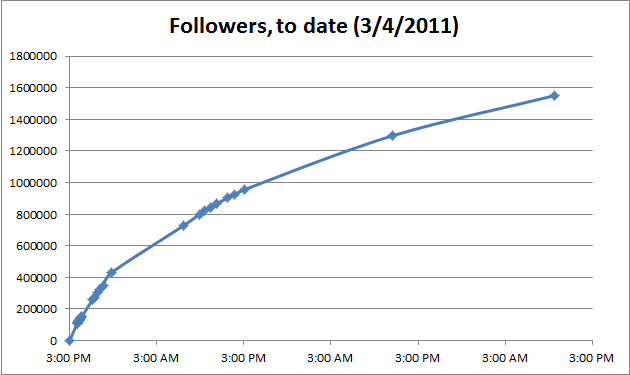Graph titled “Followers, to date (3/4/2011). Vertical measures number of followers, in increments of 200,000, from 0 to 1,800,000. Horizontal measures time, in increments of 12 hours from 3:00PM 3/1 to 3:00PM 3/4. The plotted points show an initially rapid curve starting to slow, though continue to grow, over time. While still climbing steadily, the curve is nowhere near as steep as it was on Day 1, which is probably to be expected. Hey, I bet the slope of the line over time would be interesting. And that would give us a clue as to where this thing is headed. Let’s break it up into (Change-in-followers per minute) vs. (time).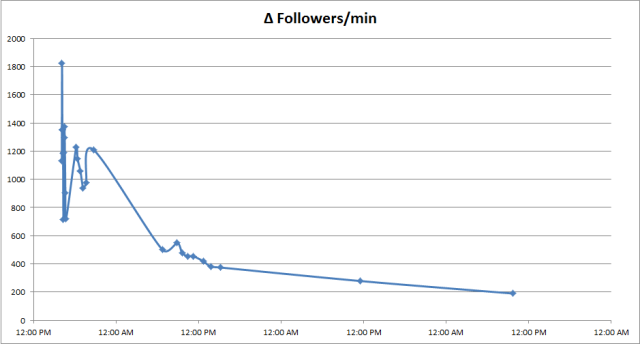Graph titled “Delta Followers/min”. Vertical measures number of followers, in increments of 200 from 0 to 2000. Horizontal measures time, in increments of 12 hours from 12:00PM over 4 days. The plotted points show large swings and spikes in the first 12 hour block, then gradual decrease over time to a smoother downward curve (though still containing minor aberrations). There’s my exponential! We’ll have to fudge the x-values a bit to get an actual equation and trendline.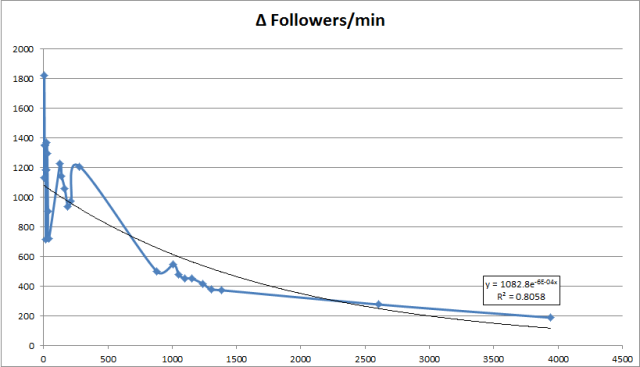Graph titled “Delta Followers/min”. Vertical measures number of followers, in increments of 200 from 0 to 2000. Horizontal measures time, in increments of 12 hours from 12:00PM over 4 days. The plotted points (in blue) show large swings and spikes in the first 12 hour block, then gradual decrease over time to a smoother downward curve (though still containing minor aberrations). Overlaid this in black is a trend line curving down, and a key: y = 1082.8e^-55.04x. R^2=0.8058. And you know what? I bet if I tossed out a few of those early, “noisy” observation, we’d get a much better fitted curve. But still, it looks like you can pretty well describe the behavior of Charlie Sheen’s number of twitter followers with this exponential decay curve. Now, what can we do with this? Was this just a ridiculous exercise by someone who spends too much time in front of his computer? Perhaps (probably). But are there any implications for the dramatic growth and tapering off of a (sort of crazy) celebrity's twitter followers? Remember in 2010, when LeBron James joined twitter before his announcement of where he was headed, dubbed “The Decision” on ESPN? His twitter followers had a similar explosion at the beginning before he even tweeted anything. I don’t have the data unfortunately. While everyone agrees that “The Decision” was a huge PR mistake, everyone also agrees that the ratings for “The Decision” were through the roof. Let’s put it this way: more people watched “The Decision” where James announced which team he would join than many actual NBA Finals games. Did the simple creation of the twitter account boost the ratings? What if “Two and a Half Men” came back on the air now? I have to assume that the ratings would be similarly boosted. James Franco did something similar before his hosting of the Oscars, joining twitter beforehand. You think agents and TV and movie execs aren’t aware of the “twitter-effect?” Of course they are, and they’re probably also interested in some of the hard data that comes along with it.

Learning Objectives

Linear and Geometric Growth
  • Build a recursive equation that models linear or exponential growth
  • Build an explicit equation that models linear or exponential growth
  • Make predictions using linear and exponential growth models
Logarithms and Logistic Growth
  • Use logarithms to solve exponential growth models for time
  • Identify the carrying capacity and growth rate of the logistic growth model
  • Use the logistic growth model to make predictions

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Can you predict how many followers @charliesheen has right now? ; Exponential growth? (Part 1). Provided by: emergent math Authored by: Geoff Krall. Located at: https://emergentmath.com/2011/03/03/can-you-predict-how-many-followers-charliesheen-has-right-now-exponential-growth-part-1/. License: CC BY-NC: Attribution-NonCommercial.
  • Can you predict how many followers @charliesheen has right now? ; Exponential growth? (Part 2). Provided by: emergent math Authored by: Geoff Krall. Located at: https://emergentmath.com/2011/03/04/can-you-predict-how-many-followers-charliesheen-has-right-now-exponential-growth-part-2/. License: CC BY-NC: Attribution-NonCommercial.
  • Learning objectives: Growth Models. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY-SA: Attribution-ShareAlike.