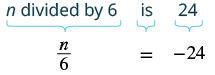We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts Corequisite

Translating Words Involving Division and Multiplication Into an Algebraic Equation and Solving

Learning Outcomes

  • Translate a phrase that contains division into an equation and solve

Translate Sentences to Equations and Solve

Recall the four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference. We will use these to solve equations that contain fractions.
Subtraction Property of Equality: For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex] if [latex]a=b[/latex], then [latex]a-c=b-c[/latex]. Addition Property of Equality: For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex] if [latex]a=b[/latex], then [latex]a+c=b+c[/latex].
Division Property of Equality: For any numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex] where [latex]\mathit{\text{c}}\ne \mathit{0}[/latex] if [latex]a=b[/latex], then [latex] \Large\frac{a}{c}= \Large\frac{b}{c}[/latex] Multiplication Property of Equality: For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c}}[/latex] if [latex]a=b[/latex], then [latex]ac=bc[/latex]
When you add, subtract, multiply or divide the same quantity from both sides of an equation, you still have equality. In the next few examples, we’ll translate sentences that contain fractions into equations and then solve the equations. The first property of equality we will use is multiplication.

Example

Translate and solve: [latex]n[/latex] divided by [latex]6[/latex] is [latex]-24[/latex]. Solution:
Translate. .
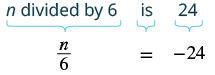Multiply both sides by [latex]6[/latex] . [latex]\color{red}{6}\cdot\Large\frac{n}{6}\normalsize=\color{red}{6}(-24)[/latex]
Simplify. [latex]n=-144[/latex]
Check: Is [latex]-144[/latex] divided by [latex]6[/latex] equal to [latex]-24[/latex] ?
Translate. [latex]\Large\frac{-144}{6}\normalsize\stackrel{?}{=}-24[/latex]
Simplify. It checks. [latex]-24=-24\quad\checkmark[/latex]

Try It

[ohm_question height="270"]146166[/ohm_question]

Example

Translate and solve: The quotient of [latex]q[/latex] and [latex]-5[/latex] is [latex]70[/latex].

Answer: Solution:

Translate. .
Multiply both sides by [latex]-5[/latex] . [latex]\color{red}{5}\Large(\frac{q}{-5}) \normalsize= \color{red}{-5}(70)[/latex]
Simplify. [latex]q=-350[/latex]
Check: Is the quotient of [latex]-350[/latex] and [latex]-5[/latex] equal to [latex]70[/latex] ?
Translate. [latex]\Large\frac{-350}{-5}\normalsize\stackrel{?}{=}70[/latex]
Simplify. It checks. [latex]70=70\quad\checkmark[/latex]

Try It

[ohm_question height="270"]146172[/ohm_question]

Example

Translate and solve: Two-thirds of [latex]f[/latex] is [latex]18[/latex].

Answer: Solution:

Translate. .
Multiply both sides by [latex]\Large\frac{3}{2}[/latex] . [latex]\color{red}{\Large\frac{3}{2}}\cdot\Large\frac{2}{3}\normalsize f=\color{red}{\Large\frac{3}{2}}\cdot \normalsize18[/latex]
Simplify. [latex]f=27[/latex]
Check: Is two-thirds of [latex]27[/latex] equal to [latex]18[/latex] ?
Translate. [latex]\Large\frac{2}{3}\normalsize(27)\normalsize\stackrel{?}{=}18[/latex]
Simplify. It checks. [latex]18=18\quad\checkmark[/latex]

try It

[ohm_question height="270"]146180[/ohm_question]

Example

Translate and solve: The quotient of [latex]m[/latex] and [latex]\Large\frac{5}{6}[/latex] is [latex]\Large\frac{3}{4}[/latex].

Answer: Solution:

The quotient of [latex]m[/latex] and [latex]\Large\frac{5}{6}[/latex] is [latex]\Large\frac{3}{4}[/latex] .
Translate. [latex]\Large\frac{m}{\LARGE\frac{5}{6}}=\Large\frac{3}{4}[/latex]
Multiply both sides by [latex]\Large\frac{5}{6}[/latex] to isolate [latex]m[/latex] . [latex]\Large\frac{5}{6}\left(\Large\frac{m}{\LARGE\frac{5}{6}}\right)=\Large\frac{5}{6}\left(\Large\frac{3}{4}\right)[/latex]
Simplify. [latex]m=\Large\frac{5\cdot 3}{6\cdot 4}[/latex]
Remove common factors and multiply. [latex]m=\Large\frac{5}{8}[/latex]
Check:
Is the quotient of [latex]\Large\frac{5}{8}[/latex] and [latex]\Large\frac{5}{6}[/latex] equal to [latex]\Large\frac{3}{4}[/latex] ? [latex]\Large\frac{\LARGE\frac{5}{8}}{\LARGE\frac{5}{6}}\stackrel{?}{=}\Large\frac{3}{4}[/latex]
Rewrite as division. [latex]\Large\frac{5}{8}\div\Large\frac{5}{6}\stackrel{?}{=}\Large\frac{3}{4}[/latex]
Multiply the first fraction by the reciprocal of the second. [latex]\Large\frac{5}{8}\cdot\Large\frac{6}{5}\stackrel{?}{=}\Large\frac{3}{4}[/latex]
Simplify. [latex]\Large\frac{3}{4}=\Large\frac{3}{4}\quad\checkmark[/latex]
Our solution checks.

Try It

[ohm_question height="270"]146184[/ohm_question]

Example

Translate and solve: The sum of three-eighths and [latex]x[/latex] is three and one-half.

Answer: Solution:

Translate. .
Use the Subtraction Property of Equality to subtract [latex]\Large\frac{3}{8}[/latex] from both sides. [latex]\Large\frac{3}{8}+\normalsize x-\Large\frac{3}{8}=\normalsize3\Large\frac{1}{2}-\Large\frac{3}{8}[/latex]
Combine like terms on the left side. [latex]x=3\Large\frac{1}{2}-\Large\frac{3}{8}[/latex]
Convert mixed number to improper fraction. [latex]x\Large\frac{7}{2}-\Large\frac{3}{8}[/latex]
Convert to equivalent fractions with LCD of [latex]8[/latex]. [latex]x=\Large\frac{28}{8}-\Large\frac{3}{8}[/latex]
Subtract. [latex]x=\Large\frac{25}{8}[/latex]
Write as a mixed number. [latex]x=3\Large\frac{1}{8}[/latex]
We write the answer as a mixed number because the original problem used a mixed number. Check: Is the sum of three-eighths and [latex]3\Large\frac{1}{8}[/latex] equal to three and one-half?
[latex]\Large\frac{3}{8}\normalsize+3\Large\frac{1}{8}\normalsize\stackrel{?}{=}3\Large\frac{1}{2}[/latex]
Add. [latex]3\Large\frac{4}{8}\normalsize\stackrel{?}{=}3\Large\frac{1}{2}[/latex]
Simplify. [latex]3\Large\frac{1}{2}\normalsize=3\Large\frac{1}{2}\quad\checkmark[/latex]
The solution checks.

try It

[ohm_question height="270"]146189[/ohm_question] [ohm_question height="270"]146199[/ohm_question]
We've seen several examples of how to translate a given mathematical relationship from words into equation form in order to solve it. Let's see some examples now that reverse the process. The following video shows examples of translating an equation into words as an aid to solving it. Note that this is different from the written examples on this page because these examples start with the mathematical equation then translate it into words. https://youtu.be/tubom5d5lxg

Licenses & Attributions

CC licensed content, Original

  • Question ID: 146166, 146172, 146180, 146184, 146189, 146199. Authored by: Alyson Day. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.

CC licensed content, Specific attribution