Equations of Ellipses
Learning Outcomes
- Identify the foci, vertices, axes, and center of an ellipse.
- Write equations of ellipses centered at the origin.
- Write equations of ellipses not centered at the origin.
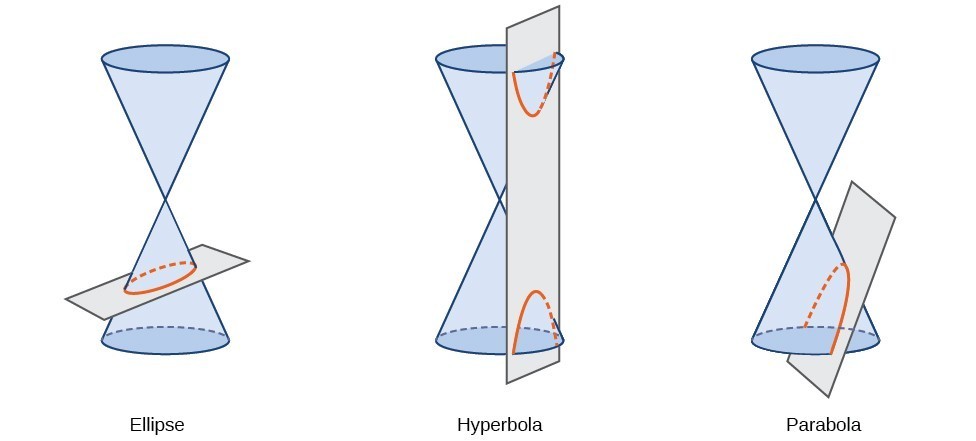 Conic sections can also be described by a set of points in the coordinate plane. Later in this chapter we will see that the graph of any quadratic equation in two variables is a conic section. The signs of the equations and the coefficients of the variable terms determine the shape. This section focuses on the four variations of the standard form of the equation for the ellipse. An ellipse is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci) of the ellipse.
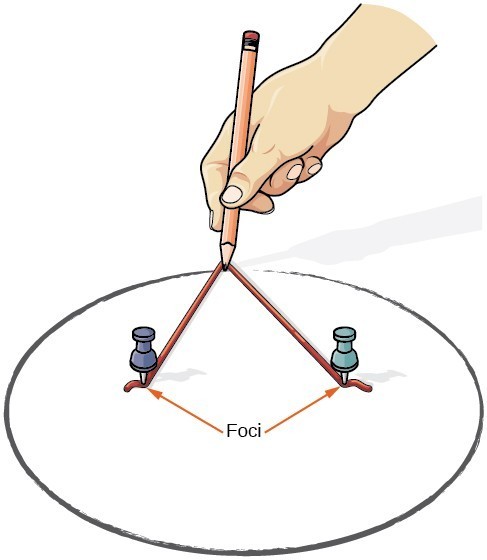
We can draw an ellipse using a piece of cardboard, two thumbtacks, a pencil, and string. Place the thumbtacks in the cardboard to form the foci of the ellipse. Cut a piece of string longer than the distance between the two thumbtacks (the length of the string represents the constant in the definition). Tack each end of the string to the cardboard, and trace a curve with a pencil held taut against the string. The result is an ellipse.
Conic sections can also be described by a set of points in the coordinate plane. Later in this chapter we will see that the graph of any quadratic equation in two variables is a conic section. The signs of the equations and the coefficients of the variable terms determine the shape. This section focuses on the four variations of the standard form of the equation for the ellipse. An ellipse is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci) of the ellipse.
We can draw an ellipse using a piece of cardboard, two thumbtacks, a pencil, and string. Place the thumbtacks in the cardboard to form the foci of the ellipse. Cut a piece of string longer than the distance between the two thumbtacks (the length of the string represents the constant in the definition). Tack each end of the string to the cardboard, and trace a curve with a pencil held taut against the string. The result is an ellipse.
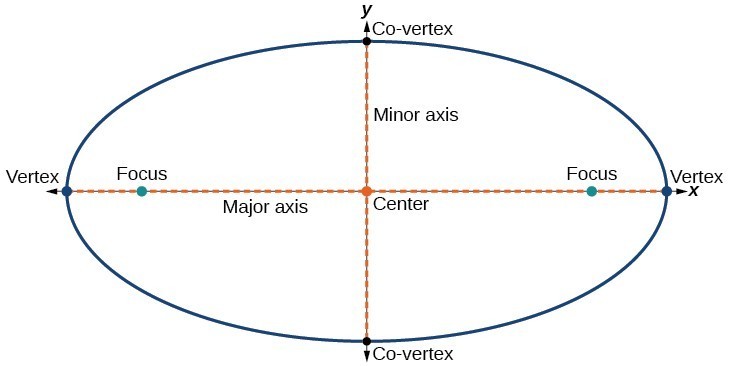
 Every ellipse has two axes of symmetry. The longer axis is called the major axis, and the shorter axis is called the minor axis. Each endpoint of the major axis is the vertex of the ellipse (plural: vertices), and each endpoint of the minor axis is a co-vertex of the ellipse. The center of an ellipse is the midpoint of both the major and minor axes. The axes are perpendicular at the center. The foci always lie on the major axis, and the sum of the distances from the foci to any point on the ellipse (the constant sum) is greater than the distance between the foci.
Every ellipse has two axes of symmetry. The longer axis is called the major axis, and the shorter axis is called the minor axis. Each endpoint of the major axis is the vertex of the ellipse (plural: vertices), and each endpoint of the minor axis is a co-vertex of the ellipse. The center of an ellipse is the midpoint of both the major and minor axes. The axes are perpendicular at the center. The foci always lie on the major axis, and the sum of the distances from the foci to any point on the ellipse (the constant sum) is greater than the distance between the foci.
 In this section we restrict ellipses to those that are positioned vertically or horizontally in the coordinate plane. That is, the axes will either lie on or be parallel to the x- and y-axes. Later in the chapter, we will see ellipses that are rotated in the coordinate plane.
To work with horizontal and vertical ellipses in the coordinate plane, we consider two cases: those that are centered at the origin and those that are centered at a point other than the origin. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. Later we will use what we learn to draw the graphs.
To derive the equation of an ellipse centered at the origin, we begin with the foci [latex](-c,0)[/latex] and [latex](-c,0)[/latex]. The ellipse is the set of all points [latex](x,y)[/latex] such that the sum of the distances from [latex](x,y)[/latex] to the foci is constant, as shown in the figure below.
In this section we restrict ellipses to those that are positioned vertically or horizontally in the coordinate plane. That is, the axes will either lie on or be parallel to the x- and y-axes. Later in the chapter, we will see ellipses that are rotated in the coordinate plane.
To work with horizontal and vertical ellipses in the coordinate plane, we consider two cases: those that are centered at the origin and those that are centered at a point other than the origin. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. Later we will use what we learn to draw the graphs.
To derive the equation of an ellipse centered at the origin, we begin with the foci [latex](-c,0)[/latex] and [latex](-c,0)[/latex]. The ellipse is the set of all points [latex](x,y)[/latex] such that the sum of the distances from [latex](x,y)[/latex] to the foci is constant, as shown in the figure below.
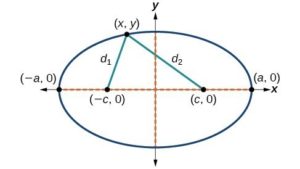
If [latex](a,0)[/latex] is a vertex of the ellipse, the distance from [latex](-c,0)[/latex] to [latex](a,0)[/latex] is [latex]a-(-c)=a+c[/latex]. The distance from [latex](c,0)[/latex] to [latex](a,0)[/latex] is [latex]a-c[/latex]. The sum of the distances from the foci to the vertex is
[latex](a+c)+(a-c)=2a[/latex]
If [latex](x,y)[/latex] is a point on the ellipse, then we can define the following variables:
[latex]\begin{align}d_1&=\text{the distance from } (-c,0) \text{ to } (x,y) \\ d_2&= \text{the distance from } (c,0) \text{ to } (x,y) \end{align}[/latex]
By the definition of an ellipse, [latex]d_1+d_2[/latex] is constant for any point [latex](x,y)[/latex] on the ellipse. We know that the sum of these distances is [latex]2a[/latex] for the vertex [latex](a,0)[/latex]. It follows that [latex]d_1+d_2=2a[/latex] for any point on the ellipse. The derivation of the standard form of the equation of an ellipse relies on this relationship and the distance formula. The derivation is beyond the scope of this course, but the equation is:
[latex]\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1[/latex]
for an ellipse centered at the origin with its major axis on the X-axis and[latex]\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1[/latex]
for an ellipse centered at the origin with its major axis on the Y-axis.Writing Equations of Ellipses Centered at the Origin in Standard Form
Standard forms of equations tell us about key features of graphs. Take a moment to recall some of the standard forms of equations we’ve worked with in the past: linear, quadratic, cubic, exponential, logarithmic, and so on. By learning to interpret standard forms of equations, we are bridging the relationship between algebraic and geometric representations of mathematical phenomena.
The key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other equations, we can identify all of these features just by looking at the standard form of the equation. There are four variations of the standard form of the ellipse. These variations are categorized first by the location of the center (the origin or not the origin), and then by the position (horizontal or vertical). Each is presented along with a description of how the parts of the equation relate to the graph. Interpreting these parts allows us to form a mental picture of the ellipse.
A General Note: Standard Forms of the Equation of an Ellipse with Center [latex](0,0)[/latex]
The standard form of the equation of an ellipse with center [latex]\left(0,0\right)[/latex] and major axis parallel to the x-axis is[latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex]
where- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(\pm a,0\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(0,\pm b\right)[/latex]
- the coordinates of the foci are [latex]\left(\pm c,0\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
[latex]\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1[/latex]
where- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(0,\pm a\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(\pm b,0\right)[/latex]
- the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
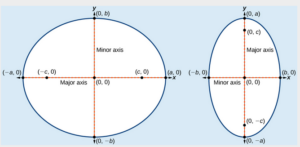 Figure: (a) Horizontal ellipse with center (0,0), (b) Vertical ellipse with center (0,0)
Figure: (a) Horizontal ellipse with center (0,0), (b) Vertical ellipse with center (0,0)How To: Given the vertices and foci of an ellipse centered at the origin, write its equation in standard form.
- Determine whether the major axis is on the x- or y-axis.
- If the given coordinates of the vertices and foci have the form [latex](\pm a,0)[/latex] and [latex](\pm c,0)[/latex] respectively, then the major axis is parallel to the x-axis. Use the standard form [latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex].
- If the given coordinates of the vertices and foci have the form [latex](0,\pm a)[/latex] and [latex](0,\pm c)[/latex] respectively, then the major axis is parallel to the y-axis. Use the standard form [latex]\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1[/latex].
- Use the equation [latex]c^2=a^2-b^2[/latex] along with the given coordinates of the vertices and foci, to solve for [latex]b^2[/latex].
- Substitute the values for [latex]a^2[/latex] and [latex]b^2[/latex] into the standard form of the equation determined in Step 1.
Example: Writing the Equation of an Ellipse Centered at the Origin in Standard Form
What is the standard form equation of the ellipse that has vertices [latex](\pm 8,0)[/latex] and foci [latex](\pm 5,0)[/latex]?Answer: The foci are on the x-axis, so the major axis is the x-axis. Thus the equation will have the form:
[latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex]
The vertices are [latex](\pm 8,0)[/latex], so [latex]a=8[/latex] and [latex]a^2=64[/latex]. The foci are [latex](\pm 5,0)[/latex], so [latex]c=5[/latex] and [latex]c^2=25[/latex]. We know that the vertices and foci are related by the equation [latex]c^2=a^2-b^2[/latex]. Solving for [latex]b^2[/latex] we have[latex]\begin{align}&c^2=a^2-b^2&& \\ &25 = 64 - b^2 && \text{Substitute for }c^2 \text{ and }a^2. \\ &b^2=39 && \text{Solve for } b^2. \end{align}[/latex]
Now we need only substitute [latex]a^2 = 64[/latex] and [latex]b^2=39[/latex] into the standard form of the equation. The equation of the ellipse is[latex]\dfrac{{x}^{2}}{64}+\dfrac{{y}^{2}}{39}=1[/latex]
try it
What is the standard form equation of the ellipse that has vertices [latex]\left(0,\pm 8\right)[/latex] and foci [latex](0,\pm \sqrt{5})[/latex]?Answer: [latex-display]x^2+\dfrac{y^2}{16}=1[/latex-display]
[ohm_question hide_question_numbers=1]156638[/ohm_question]Writing Equations of Ellipses Not Centered at the Origin
Like the graphs of other equations, the graph of an ellipse can be translated. If an ellipse is translated [latex]h[/latex] units horizontally and [latex]k[/latex] units vertically, the center of the ellipse will be [latex]\left(h,k\right)[/latex]. This translation results in the standard form of the equation we saw previously, with [latex]x[/latex] replaced by [latex]\left(x-h\right)[/latex] and y replaced by [latex]\left(y-k\right)[/latex].tip for success
Writing equations of ellipses not centered at the origin uses several concepts that you've built up for yourself over the entirety of this course such as transformations of graphs, rational equations, and the midpoint formula, to name a few. Remember that you can return to earlier module sections at any time if you need a refresher. As always, give yourself plenty of time to apply patient, repeated study of the examples and practice problems below.A General Note: Standard Forms of the Equation of an Ellipse with Center (h, k)
The standard form of the equation of an ellipse with center [latex]\left(h,\text{ }k\right)[/latex] and major axis parallel to the x-axis is[latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex]
where- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(h\pm a,k\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(h,k\pm b\right)[/latex]
- the coordinates of the foci are [latex]\left(h\pm c,k\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
[latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex]
where- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(h,k\pm a\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(h\pm b,k\right)[/latex]
- the coordinates of the foci are [latex]\left(h,k\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
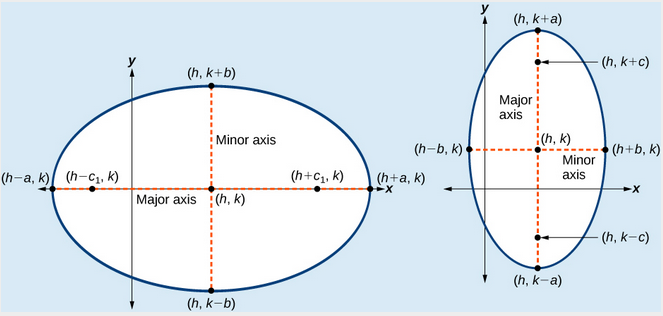 (a) Horizontal ellipse with center [latex]\left(h,k\right)[/latex] (b) Vertical ellipse with center [latex]\left(h,k\right)[/latex]
(a) Horizontal ellipse with center [latex]\left(h,k\right)[/latex] (b) Vertical ellipse with center [latex]\left(h,k\right)[/latex]How To: Given the vertices and foci of an ellipse not centered at the origin, write its equation in standard form.
- Determine whether the major axis is parallel to the x- or y-axis.
- If the y-coordinates of the given vertices and foci are the same, then the major axis is parallel to the x-axis. Use the standard form [latex]\dfrac{{\left(x-h\right)}^{2}}{{a}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{b}^{2}}=1[/latex].
- If the x-coordinates of the given vertices and foci are the same, then the major axis is parallel to the y-axis. Use the standard form [latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex].
- Identify the center of the ellipse [latex]\left(h,k\right)[/latex] using the midpoint formula and the given coordinates for the vertices.
- Find [latex]{a}^{2}[/latex] by solving for the length of the major axis, [latex]2a[/latex], which is the distance between the given vertices.
- Find [latex]{c}^{2}[/latex] using [latex]h[/latex] and [latex]k[/latex], found in Step 2, along with the given coordinates for the foci.
- Solve for [latex]{b}^{2}[/latex] using the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
- Substitute the values for [latex]h,k,{a}^{2}[/latex], and [latex]{b}^{2}[/latex] into the standard form of the equation determined in Step 1.
Example: Writing the Equation of an Ellipse Centered at a Point Other Than the Origin
What is the standard form equation of the ellipse that has vertices [latex]\left(-2,-8\right)[/latex] and [latex]\left(-2,\text{2}\right)[/latex] and foci [latex]\left(-2,-7\right)[/latex] and [latex]\left(-2,\text{1}\right)?[/latex]Answer: The x-coordinates of the vertices and foci are the same, so the major axis is parallel to the y-axis. Thus, the equation of the ellipse will have the form
[latex]\dfrac{{\left(x-h\right)}^{2}}{{b}^{2}}+\dfrac{{\left(y-k\right)}^{2}}{{a}^{2}}=1[/latex]
First, we identify the center, [latex]\left(h,k\right)[/latex]. The center is halfway between the vertices, [latex]\left(-2,-8\right)[/latex] and [latex]\left(-2,\text{2}\right)[/latex]. Applying the midpoint formula, we have:[latex]\begin{align}\left(h,k\right)&=\left(\dfrac{-2+\left(-2\right)}{2},\dfrac{-8+2}{2}\right) \\ &=\left(-2,-3\right) \end{align}[/latex]
Next, we find [latex]{a}^{2}[/latex]. The length of the major axis, [latex]2a[/latex], is bounded by the vertices. We solve for [latex]a[/latex] by finding the distance between the y-coordinates of the vertices.[latex]\begin{align}2a&=2-\left(-8\right)\\ 2a&=10\\ a&=5\end{align}[/latex]
So [latex]{a}^{2}=25[/latex]. Now we find [latex]{c}^{2}[/latex]. The foci are given by [latex]\left(h,k\pm c\right)[/latex]. So, [latex]\left(h,k-c\right)=\left(-2,-7\right)[/latex] and [latex]\left(h,k+c\right)=\left(-2,\text{1}\right)[/latex]. We substitute [latex]k=-3[/latex] using either of these points to solve for [latex]c[/latex].[latex]\begin{gathered}k+c=1\\ -3+c=1\\ c=4\end{gathered}[/latex] So [latex]{c}^{2}=16[/latex].
Next, we solve for [latex]{b}^{2}[/latex] using the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].[latex]\begin{gathered}^{2}={a}^{2}-{b}^{2}\\ 16=25-{b}^{2}\\ {b}^{2}=9\end{gathered}[/latex]
Finally, we substitute the values found for [latex]h,k,{a}^{2}[/latex], and [latex]{b}^{2}[/latex] into the standard form equation for an ellipse:[latex]\dfrac{{\left(x+2\right)}^{2}}{9}+\dfrac{{\left(y+3\right)}^{2}}{25}=1[/latex]
tip for success
These problems are too large to carry in your head all the way through. Be sure to work them out on paper. Try to list the steps in such a way that you can use a mnemonic to memorize the process.Try It
What is the standard form equation of the ellipse that has vertices [latex]\left(-3,3\right)[/latex] and [latex]\left(5,3\right)[/latex] and foci [latex]\left(1 - 2\sqrt{3},3\right)[/latex] and [latex]\left(1+2\sqrt{3},3\right)?[/latex]Answer: [latex-display]\dfrac{{\left(x - 1\right)}^{2}}{16}+\dfrac{{\left(y - 3\right)}^{2}}{4}=1[/latex-display]
[embed]Solving Applied Problems Involving Ellipses
Many real-world situations can be represented by ellipses, including orbits of planets, satellites, moons and comets, and shapes of boat keels, rudders, and some airplane wings. A medical device called a lithotripter uses elliptical reflectors to break up kidney stones by generating sound waves. Some buildings, called whispering chambers, are designed with elliptical domes so that a person whispering at one focus can easily be heard by someone standing at the other focus. This occurs because of the acoustic properties of an ellipse. When a sound wave originates at one focus of a whispering chamber, the sound wave will be reflected off the elliptical dome and back to the other focus. In the whisper chamber at the Museum of Science and Industry in Chicago, two people standing at the foci—about 43 feet apart—can hear each other whisper.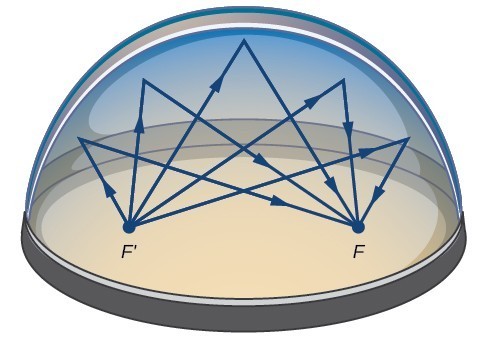
Example: Locating the Foci of a Whispering Chamber
The Statuary Hall in the Capitol Building in Washington, D.C. is a whispering chamber. Its dimensions are 46 feet wide by 96 feet long. a. What is the standard form of the equation of the ellipse representing the outline of the room? Hint: assume a horizontal ellipse, and let the center of the room be the point [latex]\left(0,0\right)[/latex]. b. If two senators standing at the foci of this room can hear each other whisper, how far apart are the senators? Round to the nearest foot.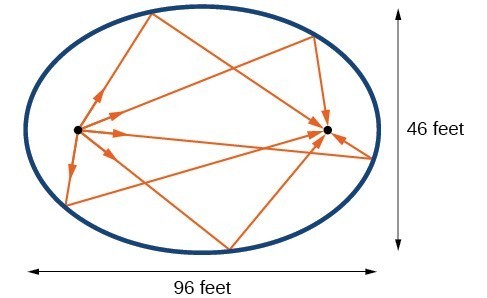
Answer: a. We are assuming a horizontal ellipse with center [latex]\left(0,0\right)[/latex], so we need to find an equation of the form [latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex], where [latex]a>b[/latex]. We know that the length of the major axis, [latex]2a[/latex], is longer than the length of the minor axis, [latex]2b[/latex]. So the length of the room, 96, is represented by the major axis, and the width of the room, 46, is represented by the minor axis.
- Solving for [latex]a[/latex], we have [latex]2a=96[/latex], so [latex]a=48[/latex], and [latex]{a}^{2}=2304[/latex].
- Solving for [latex]b[/latex], we have [latex]2b=46[/latex], so [latex]b=23[/latex], and [latex]{b}^{2}=529[/latex].
[latex]\begin{align}&{c}^{2}={a}^{2}-{b}^{2} \\ &{c}^{2}=2304 - 529 && \text{Substitute using the values found in part (a)}. \\ &c=\pm \sqrt{2304 - 529} && \text{Take the square root of both sides}. \\ &c=\pm \sqrt{1775} && \text{Subtract}. \\ &c\approx \pm 42 && \text{Round to the nearest foot}. \end{align}[/latex]
The points [latex]\left(\pm 42,0\right)[/latex] represent the foci. Thus, the distance between the senators is [latex]2\left(42\right)=84[/latex] feet.tip for success
Don't be discouraged if it takes several tries through the example and practice problem to understand the process. These problems are challenging, but you can achieve success with time and effort.Try It
Suppose a whispering chamber is 480 feet long and 320 feet wide. a. What is the standard form of the equation of the ellipse representing the room? Hint: assume a horizontal ellipse, and let the center of the room be the point [latex]\left(0,0\right)[/latex]. b. If two people are standing at the foci of this room and can hear each other whisper, how far apart are the people? Round to the nearest foot.Answer: a. [latex]\dfrac{{x}^{2}}{57,600}+\dfrac{{y}^{2}}{25,600}=1[/latex] b. The people are standing 358 feet apart.
[embed]Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 1667. Authored by: WebWork-Rochester, mb Sousa,James. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 87055. Authored by: Shahbazian,Roy. License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. License: CC BY: Attribution.
