Reading: Curve Sketching
Maxima and Minima of Functions
Much can be done to sketch the approximate graph of a function without calculus, in fact I strongly encourage you to rely mostly on your pre-calculus skills to sketch graphs. But by adding the derivative and second derivative to our toolbox, we can determine the exact locations of maxima and minima (collectively "extrema") of a function, and more. First a little terminology:More Terminology
A global maximum or minimum might sometimes be called "local." Think of it like the Venn diagram in figure 2. Global maxima and minima are a subset of local maxima and minima. On a given interval of the domain of a function, there can be only one global (or absolute) max. and min.—if either exists. Remember that the derivative, f ′(x), of the function f(x) gives the slope of f(x) at any differentiable point in its domain. The derivative of a rising function (positive slope) is positive, and the derivative of a falling function (negative slope) is negative. In the middle case, where the slope is zero, the function graph is neither rising nor falling, but is (usually) a relative maximum or minimum value. Fermat's theorem sums this up: Fermat's theorem says that if a function has a local maximum or minimum (which could be global), then the derivative at that point is zero.Proof
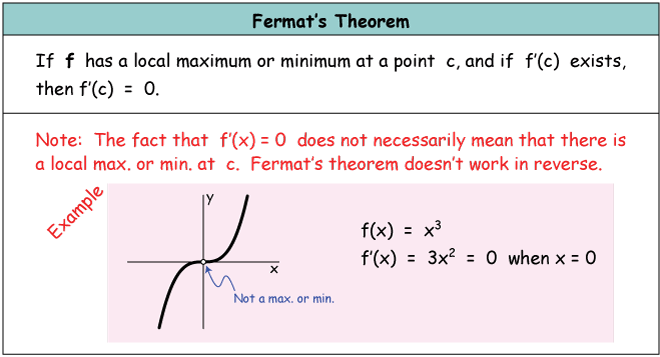
Referring to the definition of the local maximum above, we see that if a maximum value lies at x = c, then f(x) must be larger than some other value of the function f(x + h), where h can be positive or negative. So: [latex] f(c) \geq f(c + h) [/latex] which rearranges to [latex] f(c + h) - f(c) \leq 0 [/latex] We can divide both sides of this inequality by h to make this look like a derivative, then take the limit as h → 0+ from the right: [latex-display] \lim_{h \to 0^+} \frac{f(c+h)-f(c)}{h} = \lim_{h \to 0^+} 0 = 0 [/latex-display] Now we have assumed that f′(c) exists, so the limit from the right must equal the limit in general: [latex-display] \lim_{h \to 0^+} \frac{f(c+h)-f(c)}{h} = \lim_{h \to 0} \frac{f(c+h)-f(c)}{h} [/latex-display] The second equation is f ′(c). Plugging f ′(c) into the last inequality, we get: f ′(c) ≤ 0 Now we could also do the same proof using the limit from the left, which would lead us to the inequality f ′(c) ≥ 0. The only way that both inequalities can be true is for f ′(c) to be equal to zero, so we have proved Fermat's theorem. Caution: Fermat's theorem doesn't necessarily work both ways. Go back and look at the Fermat's theorem box above and make sure to understand that the existence of a zero in the derivative function does not guarantee the existence of a relative or global max. or min. there. The graph of y = x3, for example, has a horizontal tangent at x = 0, but it has no maxima or minima at all. Here's a summary of the relationships of the first derivative of a function to maxima and minima (either local or global) in its graph:Example 1
Find the x-coordinates of the maxima and minima of f(x) = −x3 + 4x2 + 4x − 16 It's very important when working these problems, not to forget your pre-calculus skills, the algebra skills you learned prior to calculus. Calculus won't replace the skills you already have, it will just enhance what you can learn about the graph of a function. Don't forget your pre-calculus curve-sketching skills. Most of curve sketching does not require (and doesn't benefit from) calculus. We begin by noting that this function can be factored by grouping: [latex-display] f(x) = -x(x^2 -4)+ 4(x^2 -4) [/latex-display] [latex-display] f(x) = (4 -x)(x^2 -4) [/latex-display] [latex] f(x) = (4 -x)(x + 2)(x - 2) [/latex] Real roots at x 4, ±2 The leading term is negative, so we know this function grows without bound on the left as x → −∞, and tends to −∞ as x → ∞ (i.e. goes up on the left and down on the right). We also know, from our familiarity with the sigmoidal (sideways-S) shape of the graphs of cubic functions, that the left-most extremum (which lies between x = −2 and x = 2, should be the local minimum and the right-most (between x = 2 and x = 4) the maximum. Here's a schematic picture: Now to find the exact positions of the min. and max. using the derivative:| The derivative | [latex] f\prime(x) = -3x^2 + 8x + 4 [/latex] |
| Set the derivative equal to zero | [latex] -3x^2 + 8x + 4 = 0 [/latex] |
| Complete the square to find the roots | [latex] -3x^2 + 8x = -4 [/latex] |
| [latex] x^2 - \frac{8}{3}x + (\frac{4}{3})^2 = \frac{16}{9} + {12}{9} [/latex] | |
| [latex] (x -\frac{4}{3})^2 = \frac{28}{9} [/latex] | |
| [latex] x = \frac{4 \pm 2 \sqrt7}{3} [/latex] | |
| Locations of the extrema | x ≈ −0.4, 3.1 |
Example 2
A cylindrical metal can is to hold 1 liter of olive oil. Find the dimensions of the can that holds 1 liter and requires the least metal possible to manufacture. Figure 7 is a schematic of the container. The top and bottom are circles of area A = πr2 and the side piece is a rectangle with area equal to the height (h) of the cylinder times its circumference, 2πr. The surface area gives us the amount of material needed to build the cylinder. We'll use cm2 as the unit of area noting that 1 liter is 1000 cm3. A = (2)(πr2) + 2πrh The surface area is a function of two variables, r and h, but we can use the known volume to substitute for h as a function of r: [latex-display] V = \pi r^2h = 1000 [/latex-display] [latex-display] h = \frac{1000}{\pi r^2} [/latex-display] Now we have a single-variable equation for the surface area of the can: [latex-display] A = (2)(\pi r^2) + \frac{2000}{r} [/latex-display] Now we assume, because of the way we constructed this formula, that it has a maximum value. Now is the time to take out your calculator to confirm that it does. Take the derivative of A(r) with respect to r and set it equal to zero: [latex-display] \frac{dA}{dt} = 4\pi r - \frac{2000}{r^2} = 0 [/latex-display] Solve for r: [latex-display] r^3 = \frac{2000}{4\pi} [/latex-display] [latex-display] r = (\frac{2000}{4\pi})^{1/3} = 5.42 \text{cm} [/latex-display] The figure below shows a comparison between a polynomial function and its derivative. I've chosen the 6th degree polynomial function f(x) = x6 − 3x5 + 6x3 − 3x2 − 3x + 2 for this comparison because it contains a variety of features, including two minima (one a global minimum), a local maximum and an inflection point. Inflection point—a point in a graph at which the curvature changes between concave-upward and concave-downward.The First Derivative
Remember that the derivative gives the slope of a function at any point in its domain. Therefore when the slope of a function is negative, like the region between −∞ and −1 for f(x), the graph of the derivative should lie below y = 0, which it does (red curve). Follow this trend across the graph, through all of its regions of negative and positive slope. Wherever the slope of f(x) is increasing the graph of the derivative is positive; likewise for decreasing regions. Next, sometimes the derivative graph passes through zero. That means f(x) has zero slope at those points. Zero is the slope of a horizontal tangent, which occurs at extrema or critical points. We always have to be careful of exceptions, however. In fact, this function has a zero in its derivative at x = 1 with no corresponding maximum or minimum there. We can use the first derivative to determine whether a particular extreme value is a maximum or a minimum:- If the slope on the left side of an extreme value is negative and that on the right is positive, the extreme value is a minimum.
- If the slope on the left side of an extreme value is positive and that on the right is negative, the extreme value is a maximum.
The Second Derivative
The second derivative is a good indicator of the curvature of a function. In this comparison, notice that every zero (f″(x) = 0) in the graph of the second derivative matches an inflection point in the graph of f(x).
The zeros in f′(x) all align with inflection points. In particular, the zero at x = 1 confirms the inflection point we already knew.
It is possible, however, that a zero in the 2nd derivative of a function does not indicate an inflection point. For example, the function g(x) = x4 has a zero at x = 0 in its second derivative, g″(x) = 12x2, but that point is actually the global minimum of that function, with concave-up curvature on either side. We must be cautious when basing conclusions about inflection points on the second derivative.
Finally, the second derivative can supply more information about whether an extremum (singular of extrema) is a relative maximum or minimum:
For an extremum at a point c in the domain of f(x),
- f″(c) > 0 for a relative minimum
- f″(c) < 0 for a relative maximum.
This is often referred to as the second derivative test.
The General Approach to Curve Sketching
Now we have another tool in our toolbox for understanding the shape of a graph: Perform the usual algebraic analysis, then use the first and second derivatives to find extrema and inflection points.- Use your pre-calculus skills: Determine whether function has any asymptotes or other discontinuities like holes, determine the behavior of the extreme ends of the function, and find any points that are easy to find—the y-intercept, for example; determine the roots (x-intercepts) if possible.
- Find the 1st the first derivative and solve f′(x) = 0 to find the critical points.
- Decide whether f′(x) is negative or positive on each interval between critical points. Make sure that this information is consistent with what you determined in steps 1 & 2.
- Find the 2nd derivative if possible (sometimes this can be a mess, so be sure you really need to!) If f″(x) > 0, the function is concave upward; if f″(x) < 0, it's concave downward. f″(x) = 0 at an inflection point (usually).
- Combine all of these steps and make sure that all of the information you have about the function is consistent. It has to be.
Example 3
Sketch an accurate graph of f(x) including the locations of any asymptotes, maxima, minima and inflection points.[latex]{f(x)}=\frac{{{x}^{2}-{2x}+{4}}}{{{x}-{2}}}[/latex]
First, we note the the numerator is quadratic, with a negative discriminant, therefore the function has no real roots and its graph doesn't cross the x-axis:[latex]{b}^{2}-{4ac}={-2}^{2}-{4(1)(-2)}={4}-{8}={-4}[/latex]
The degree of the numerator (2) exceeds the degree of the denominator (1) by one, so the function has a slant asymptote. We find its equation by polynomial division, then note that the denominator has a zero at x = 2, therefore the function has a vertical asymptote there.


 Figure 11
Figure 11Example 4
Sketch an accurate graph of f(x) including the locations of any asymptotes, maxima, minima and inflection points.
![]()
The y-intercept is often very easy to calculate, so don't ignore it. Now we note the the degree of the denominator is one less than that of the numerator, so we expect a slanted asymptote, and we find its equation by polynomial division:

 Setting the derivative equal to zero (below) , and solving by completing the square shows us that there are no real solutions, thus there are no places on the curve with a horizontal tangent slope—no maxima or minima at all:
Setting the derivative equal to zero (below) , and solving by completing the square shows us that there are no real solutions, thus there are no places on the curve with a horizontal tangent slope—no maxima or minima at all:
 Here is the graph of f(x).
This example is another good reminder not to forget about those precalculus skills. We found the y-intercept, the equation of the slant asymptote and the roots using algebra, and the facts they revealed basically established the shape of the graph. It's also worth thinking about the relative simplicity of the function—it just cant have a tremendous number of "wiggles" because its highest power is 2.
We used the first derivative to establish that there were no maxima or minima, sealing the deal on the shape of the graph; without any turning points and the other constraints we've stacked up, we've got all of the important features needed to sketch the graph. Absence of maxima or minima allows us to conclude that this function does not cross the slant asymptote for x near zero. If it did, that would create a "bump."
Here is the graph of f(x).
This example is another good reminder not to forget about those precalculus skills. We found the y-intercept, the equation of the slant asymptote and the roots using algebra, and the facts they revealed basically established the shape of the graph. It's also worth thinking about the relative simplicity of the function—it just cant have a tremendous number of "wiggles" because its highest power is 2.
We used the first derivative to establish that there were no maxima or minima, sealing the deal on the shape of the graph; without any turning points and the other constraints we've stacked up, we've got all of the important features needed to sketch the graph. Absence of maxima or minima allows us to conclude that this function does not cross the slant asymptote for x near zero. If it did, that would create a "bump."
Example 5
Sketch the graph of the function f(x) = x3 − 2x2 − 5x + 6 First, try to factor such a function; it could make life easier. This function can't be factored by grouping, but the rational root theorem, with a guess of x = 1 gets us to a factorable quadratic:

 The two methods are in agreement.
The function looks like the graph in figure 13, and all of our discoveries, roots, y-intercept, and the relative maximum and relative minimum, are in the right place.
The two methods are in agreement.
The function looks like the graph in figure 13, and all of our discoveries, roots, y-intercept, and the relative maximum and relative minimum, are in the right place.
Example 6
Explore the graph of the absolute-value function![]() .
.

Solution
According to the differentiation formula, f′(x) is:

Example 7
Sketch the graph of the function f(x) = 3x1/3 We know the general shape of a root function, but recall that we can find odd roots of negative numbers, so this function is somewhat S-shaped. Take the first derivative and notice that it is greater than zero for all x, and x can't be equal to zero. So this function is increasing throughout its domain, which includes zero, but its slope is undefined at zero.![]()

Licenses & Attributions
CC licensed content, Shared previously
- Curve Sketching. Authored by: Dr. Jeff Cruzan. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike.