We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Boundless Calculus

Inverse Functions: Exponential, Logarithmic, and Trigonometric Functions

Inverse Functions

An inverse function is a function that undoes another function.

Learning Objectives

Discuss what it means to be an inverse function

Key Takeaways

Key Points

  • If an input [latex]x[/latex] into the function [latex]f[/latex] produces an output [latex]y[/latex], then putting [latex]y[/latex] into the inverse function [latex]g[/latex] produces the output [latex]x[/latex], and vice versa (i.e., [latex]f(x)=y[/latex], and [latex]g(y)=x[/latex]).
  • A function [latex]f[/latex] that has an inverse is called invertible; the inverse function is then uniquely determined by [latex]f[/latex] and is denoted by [latex]f^{-1}[/latex].
  • If [latex]f[/latex] is invertible, the function [latex]g[/latex] is unique; in other words, there is exactly one function [latex]g[/latex] satisfying this property (no more, no fewer).

Key Terms

  • inverse: a function that undoes another function
  • function: a relation in which each element of the domain is associated with exactly one element of the co-domain
An inverse function is a function that undoes another function. If an input [latex]x[/latex] into the function [latex]f[/latex] produces an output [latex]y[/latex], then putting [latex]y[/latex] into the inverse function [latex]g[/latex] produces the output [latex]x[/latex], and vice versa (i.e., [latex]f(x)=y[/latex], and [latex]g(y)=x[/latex] ). More directly, [latex]g(f(x))=x[/latex], meaning [latex]g(x)[/latex] composed with [latex]f(x)[/latex], leaves [latex]x[/latex] unchanged. A function [latex]f[/latex] that has an inverse is called invertible; the inverse function is then uniquely determined by [latex]f[/latex] and is denoted by [latex]f^{-1}[/latex].
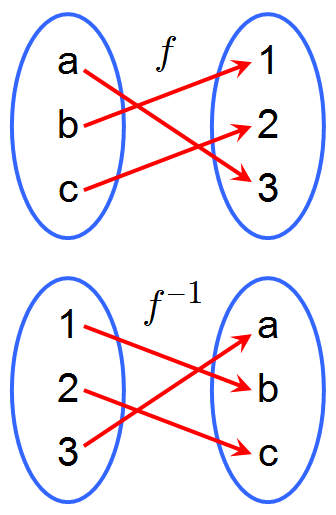
image

A Function and its Inverse: A function [latex]f[/latex] and its inverse, [latex]f^{-1}[/latex]. Because [latex]f[/latex] maps [latex]a[/latex] to [latex]3[/latex], the inverse [latex]f^{-1}[/latex] maps [latex]3[/latex] back to [latex]a[/latex].

Instead of considering the inverses for individual inputs and outputs, one can think of the function as sending the whole set of inputs—the domain —to a set of outputs—the range. Let [latex]f[/latex] be a function whose domain is the set [latex]X[/latex] and whose range is the set [latex]Y[/latex]. Then [latex]f[/latex] is invertible if there exists a function [latex]g[/latex] with domain [latex]Y[/latex] and range [latex]X[/latex], with the following property: [latex-display]f (x) = y \Leftrightarrow g (y) = x[/latex-display]
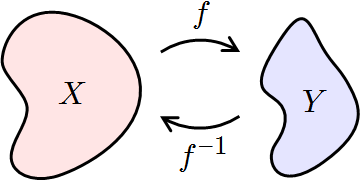
image

Inverse Functions: If [latex]f[/latex] maps [latex]X[/latex] to [latex]Y[/latex], then [latex]f^{-1}[/latex]  maps [latex]Y[/latex] back to [latex]X[/latex].

If [latex]f[/latex] is invertible, the function [latex]g[/latex] is unique; in other words, there is exactly one function [latex]g[/latex] satisfying this property (no more, no fewer). That function [latex]g[/latex] is then called the inverse of [latex]f[/latex], and is usually denoted as [latex]f^{-1}[/latex]. Stated otherwise, a function is invertible if and only if its inverse relation is a function on the range [latex]Y[/latex], in which case the inverse relation is the inverse function. Not all functions have an inverse. For this rule to be applicable, each element [latex]y \in Y[/latex] must correspond to no more than one [latex]x \in X[/latex]; a function [latex]f[/latex] with this property is called one-to-one, information-preserving, or an injection.

Example

Let's take the function [latex]y=x^2+2[/latex]. To find the inverse of this function, undo each of the operations on the [latex]x[/latex] side of the equation one at a time. We start with the [latex]+2[/latex] operation. Notice that we start in the opposite order of the normal order of operations when we undo operations. The opposite of [latex]+2[/latex] is [latex]-2[/latex]. We are left with [latex]x^2[/latex]. To undo use the square root operation. Thus, the inverse of [latex]x^2+2[/latex] is [latex]\sqrt{x-2}[/latex]. We can check to see if this inverse "undoes" the original function by plugging that function in for [latex]x[/latex]: [latex-display]\sqrt{\left(x^2+2\right)-2}=\sqrt{x^2}=x[/latex-display]

Derivatives of Exponential Functions

The derivative of the exponential function is equal to the value of the function.

Learning Objectives

Solve for the derivatives of exponential functions

Key Takeaways

Key Points

  • [latex]e^x[/latex] is its own derivative: [latex]\frac{d}{dx}e^{x} = e^{x}[/latex].
  • If a variable 's growth or decay rate is proportional to its size, then the variable can be written as a constant times an exponential function of time.
  • For any differentiable function [latex]f(x)[/latex], [latex]\frac{d}{dx}e^{f(x)} = f'(x)e^{f(x)}[/latex].

Key Terms

  • exponential: any function that has an exponent as an independent variable
  • tangent: a straight line touching a curve at a single point without crossing it there
  • e: the base of the natural logarithm, [latex]2.718281828459045\dots[/latex]
The importance of the exponential function in mathematics and the sciences stems mainly from properties of its derivative. In particular: [latex-display]\dfrac{d}{dx}e^{x} = e^{x}[/latex-display] That is to say, [latex]e^x[/latex] is its own derivative.
image

Graph of an Exponential Function: Graph of the exponential function illustrating that its derivative is equal to the value of the function. From any point [latex]P[/latex] on the curve (blue), let a tangent line (red), and a vertical line (green) with height [latex]h[/latex] be drawn, forming a right triangle with a base [latex]b[/latex] on the [latex]x[/latex]-axis. Since the slope of the red tangent line (the derivative) at [latex]P[/latex] is equal to the ratio of the triangle's height to the triangle's base (rise over run), and the derivative is equal to the value of the function, [latex]h[/latex] must be equal to the ratio of [latex]h[/latex] to [latex]b[/latex]. Therefore, the base [latex]b[/latex] must always be [latex]1[/latex].

Functions of the form [latex]ce^x[/latex] for constant [latex]c[/latex] are the only functions with this property. Other ways of saying this same thing include:
  • The slope of the graph at any point is the height of the function at that point.
  • The rate of increase of the function at [latex]x[/latex] is equal to the value of the function at [latex]x[/latex].
  • The function solves the differential equation [latex]y' = y [/latex].
  • [latex]e^x[/latex] is a fixed point of derivative as a functional.
If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth, continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time. Explicitly for any real constant [latex]k[/latex], a function [latex]f: R→R[/latex] satisfies [latex]f′ = kf [/latex] if and only if [latex]f(x) = ce^{kx}[/latex] for some constant [latex]c[/latex]. Furthermore, for any differentiable function [latex]f(x)[/latex], we find, by the chain rule: [latex-display]\displaystyle{\frac{d}{dx}e^{f(x)} = f'(x)e^{f(x)}}[/latex-display]

Logarithmic Functions

The logarithm of a number is the exponent by which another fixed value must be raised to produce that number.

Learning Objectives

Demonstrate that logarithmic functions are the inverses of exponential functions

Key Takeaways

Key Points

  • The idea of logarithms is to reverse the operation of exponentiation, that is raising a number to a power.
  • A naive way of defining the logarithm of a number [latex]x[/latex] with respect to base [latex]b[/latex] is the exponent by which [latex]b[/latex] must be raised to yield [latex]x[/latex].
  • To define the logarithm, the base [latex]b[/latex] must be a positive real number not equal to [latex]1[/latex] and [latex]x[/latex] must be a positive number.

Key Terms

  • binary: the bijective base-2 numeral system, which uses only the digits 0 and 1
  • exponent: the power to which a number, symbol or expression is to be raised: for example, the [latex]3[/latex] in [latex]x^3[/latex].
The logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: 1000 = 10 10 10 = 103. More generally, if [latex]x = b^y[/latex], then [latex]y[/latex] is the logarithm of [latex]x[/latex] to base [latex]b[/latex], and is written [latex]y=\log_b(x)[/latex], so [latex]\log_{10}(1000)=3[/latex] log10(1000) = 3. The logarithm to base [latex]b = 10[/latex] is called the common logarithm and has many applications in science and engineering. The natural logarithm has the constant [latex]e[/latex] ([latex]\approx 2.718[/latex]) as its base; its use is widespread in pure mathematics, especially calculus. The binary logarithm uses base [latex]b = 2[/latex] and is prominent in computer science. The idea of logarithms is to reverse the operation of exponentiation, that is raising a number to a power. For example, the third power (or cube) of 2 is 8, because 8 is the product of three factors of 2: [latex]2^{3} = 2 \times 2\times 2 = 8[/latex]. It follows that the logarithm of 8 with respect to base 2 is 3, so log2 8 = 3.
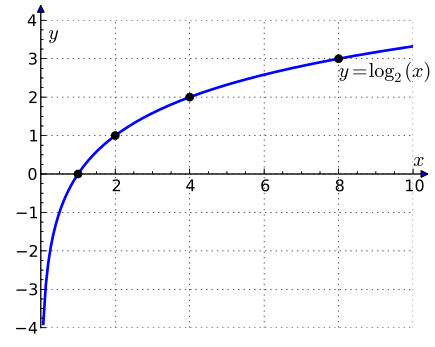
image

Plot of [latex]\log_2(x)[/latex]: The graph of the logarithm to base 2 crosses the x-axis (horizontal axis) at 1 and passes through the points with coordinates (2, 1), (4, 2), and (8, 3). For example, log2(8) = 3, because 23 = 8. The graph gets arbitrarily close to the y axis, but does not meet or intersect it.

A naive way of defining the logarithm of a number [latex]x[/latex] with respect to base b is the exponent by which b must be raised to yield x. In other words, the logarithm of [latex]x[/latex] to base b is the solution y to the equation: [latex]b^{y} = x[/latex]. This definition assumes that we know exactly what we mean by 'raising a real positive number to a real power'. Raising to integer powers is easy. It is clear that two raised to the third is eight, because 2 multiplied by itself 3 times is 8, so the logarithm of eight with respect to base two will be 3. However, the definition also assumes that we know how to raise numbers to non-integer powers. What would be the logarithm of ten? The definition tells us that the binary logarithm of ten is 3.3219 because two raised to the 3.3219th power is ten. So, the definition only makes sense if we know how to multiply 2 by itself 3.3219 times. For the definition to work, it must be understood that ' raising two to the 0.3219 power' means 'raising the 10000th root of 2 to the 3219th power'. The ten-thousandth root of 2 is 1.0000693171 and this number raised to the 3219th power is 1.2500, therefore ' 2 multiplied by itself 3.3219 times' will be 2 x 2 x 2 x 1.2500 namely 10. Making this proviso, if the base b is any positive number except 1, and the number [latex]x[/latex] is greater than zero, there is always a real number y that solves the equation: [latex]b^{y} = x[/latex] so the logarithm is well defined. The logarithm is denoted "logb(x)". In the equation y = logb(x), the value y is the answer to the question "To what power must b be raised, in order to yield x?". To define the logarithm, the base b must be a positive real number not equal to 1 and x must be a positive number.

Derivatives of Logarithmic Functions

The general form of the derivative of a logarithmic function is [latex]\frac{d}{dx}\log_{b}(x) = \frac{1}{xln(b)}[/latex].

Learning Objectives

Solve for the derivative of a logarithmic function

Key Takeaways

Key Points

  • The derivative of natural logarithmic function is [latex]\frac{d}{dx}\ln(x) = \frac{1}{x}[/latex].
  • The general form of the derivative of a logarithmic function can be derived from the derivative of a natural logarithmic function.
  • Properties of the logarithm can be used to to differentiate more difficult functions, such as products with many terms, quotients of composed functions, or functions with variable or function exponents.

Key Terms

  • logarithm: the exponent by which another fixed value, the base, must be raised to produce that number
  • e: the base of the natural logarithm, [latex]2.718281828459045\dots[/latex]
Here, we will cover derivatives of logarithmic functions. First, we will derive the equation for a specific case (the natural log, where the base is [latex]e[/latex]), and then we will work to generalize it for any logarithm. Let us create a variable [latex]y[/latex] such that [latex]y = \ln (x)[/latex]. It should be noted that what we want is the derivative of y, or [latex]\frac{dy}{dx}[/latex]. Next, we will raise both sides to the power of [latex]e[/latex] in an attempt to remove the logarithm from the right hand side: [latex-display]e^{y} = x[/latex-display] Applying the chain rule and the property of exponents we derived earlier, we can take the derivative of both sides: [latex-display]\dfrac{dy}{dx} \cdot e^{y} = 1[/latex-display] This leaves us with the derivative [latex-display]\dfrac{dy}{dx} = \dfrac{1}{e^{y}}[/latex-display] Substituting back our original equation of [latex]x = e^{y}[/latex], we find that [latex-display]\dfrac{d}{dx}\ln(x) = \dfrac{1}{x}[/latex-display] If we wanted, we could go through that same process again for a generalized base, but it is easier just to use properties of logs and realize that [latex-display]\log_{b}(x) = \dfrac{\ln(x)}{\ln(b)}[/latex-display] Since [latex]\frac{1}{\ln(b)}[/latex] is a constant, we can take it out of the derivative: [latex]\dfrac{d}{dx}\log_{b}(x) = \dfrac{1}{\ln(b)} \cdot \dfrac{d}{dx}\ln(x)[/latex], which leaves us with the generalized form of: [latex-display]\dfrac{d}{dx}\log_{b}(x) = \dfrac{1}{x \ln(b)}[/latex-display] We can use the properties of the logarithm, particularly the natural log, to differentiate more difficult functions, such as products with many terms, quotients of composed functions, or functions with variable or function exponents. We do this by taking the natural logarithm of both sides and re-arranging terms using the following logarithm laws:
  • [latex]\log \left(\dfrac{a}{b}\right) = \log (a) - \log (b)[/latex]
  • [latex]\log(a^{n}) = n \log(a)[/latex]
  • [latex]\log(a) + \log (b) = \log(ab)[/latex]
and then differentiating both sides implicitly, before multiplying through by [latex]y[/latex].

The Natural Logarithmic Function: Differentiation and Integration

Differentiation and integration of natural logarithms is based on the property [latex]\frac{d}{dx}\ln(x) = \frac{1}{x}[/latex].

Learning Objectives

Practice integrating and differentiating the natural logarithmic function

Key Takeaways

Key Points

  • The natural logarithm allows simple integration of functions of the form [latex]g(x) = \frac{ f '(x)}{f(x)}[/latex].
  • The natural logarithm can be integrated using integration by parts: [latex]\int\ln(x)dx=x \ln(x)−x+C[/latex].
  • The derivative of the natural logarithm leads to the Taylor series for [latex]\ln(1 + x)[/latex] around [latex]0[/latex]: [latex]\ln(1+x) = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \cdots[/latex] for [latex]\left | x \right | \leq 1[/latex] (unless [latex]x = -1[/latex]).

Key Terms

  • transcendental: of or relating to a number that is not the root of any polynomial that has positive degree and rational coefficients
  • irrational: of a real number, that cannot be written as the ratio of two integers
The natural logarithm, generally written as [latex]\ln(x)[/latex], is the logarithm with the base e, where e is an irrational and transcendental constant approximately equal to [latex]2.718281828[/latex]. The derivative of the natural logarithm is given by: [latex-display]\dfrac{d}{dx}\ln(x) = \dfrac{1}{x}[/latex-display] This leads to the Taylor series for [latex]\ln(1 + x)[/latex] around [latex]0[/latex]: [latex-display]\ln(1+x) = x - \dfrac{x^{2}}{2} + \dfrac{x^{3}}{3} - \cdots[/latex-display] for [latex]\left | x \right | \leq 1[/latex] (unless [latex]x = -1[/latex]).
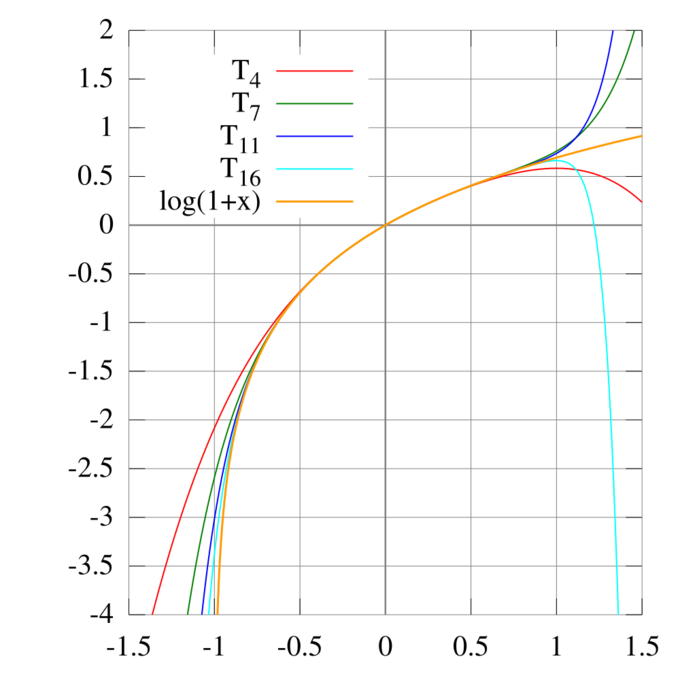
image

Taylor Series Approximations for [latex]\ln(1+x)[/latex]: The Taylor polynomials for [latex]\ln(1 + x)[/latex] only provide accurate approximations in the range [latex]-1 < x \leq 1[/latex]. Note that, for [latex]x>1[/latex], the Taylor polynomials of higher degree are worse approximations.

Substituting [latex]x − 1[/latex] for [latex]x[/latex], we obtain an alternative form for [latex]\ln(x)[/latex] itself: [latex-display]\ln(x) = (x - 1) - \dfrac{(x - 1)^{2}}{2} + \dfrac{(x - 1)^{3}}{3} - \cdots[/latex-display] for [latex]\left | x -1 \right | \leq 1[/latex] (unless [latex]x = 0[/latex]). By using Euler transform, we reach the following equation, which is valid for any [latex]x[/latex] with absolute value greater than [latex]1[/latex]: [latex-display]\ln\dfrac{x}{x-1} = \dfrac{1}{x} + \dfrac{1}{2x^{2}} + \dfrac{1}{3x^{3}} +...[/latex-display] The natural logarithm allows simple integration of functions of the form [latex]g(x) = \frac{f '(x)}{f(x)}[/latex]: an antiderivative of [latex]g(x)[/latex] is given by [latex]\ln\left(\left|f(x)\right|\right)[/latex]. This is the case because of the chain rule and the following fact: [latex-display]\dfrac{d}{dx}\left(\ln\left | x \right |\right) = \dfrac{1}{x}[/latex-display] In other words: [latex-display]\displaystyle{\int \dfrac{1}{x}dx = \ln\left | x \right | + C}[/latex-display] and [latex-display]\int \frac{f'(x)}{f(x)}dx = ln\left | f(x) \right | + C[/latex-display] Here is an example in the case of [latex]g(x) = \tan(x)[/latex]: [latex-display]\displaystyle{\int \tan (x)dx = \int \frac{\sin (x)}{\cos (x)}dx}[/latex-display] [latex-display]\displaystyle{\int \tan (x)dx = \int \frac{\frac{-d}{dx}cos (x)}{\cos (x)}dx}[/latex-display] Letting [latex]f(x) = \cos(x)[/latex] and [latex]f'(x)= – \sin(x)[/latex]: [latex-display]\displaystyle{\int \tan (x)dx = -\ln\left | \cos(x) \right | + C}[/latex-display] where [latex]C[/latex] is an arbitrary constant of integration. The natural logarithm can be integrated using integration by parts: [latex-display]\displaystyle{\int \ln(x)dx = x\ln(x) - x + C}[/latex-display]

The Natural Exponential Function: Differentiation and Integration

The derivative of the exponential function [latex]\frac{d}{dx}a^x = \ln(a)a^{x}[/latex].

Learning Objectives

Practice integrating and differentiating the natural exponential function

Key Takeaways

Key Points

  • The formula for differentiation of exponential function [latex]a^{x}[/latex] can be derived from a specific case of natural exponential function [latex]e^{x}[/latex].
  • The derivative of the natural exponential function [latex]e^{x}[/latex] is expressed as [latex]\frac{d}{dx}e^{x} =e^{x}[/latex].
  • The integral of the natural exponential function [latex]e^{x}[/latex] is [latex]\int e^{x}dx = e^{x} + C[/latex].

Key Terms

  • differentiation: the process of determining the derived function of a function
  • e: the base of the natural logarithm, [latex]2.718281828459045\dots[/latex]
Here we consider differentiation of natural exponential functions.
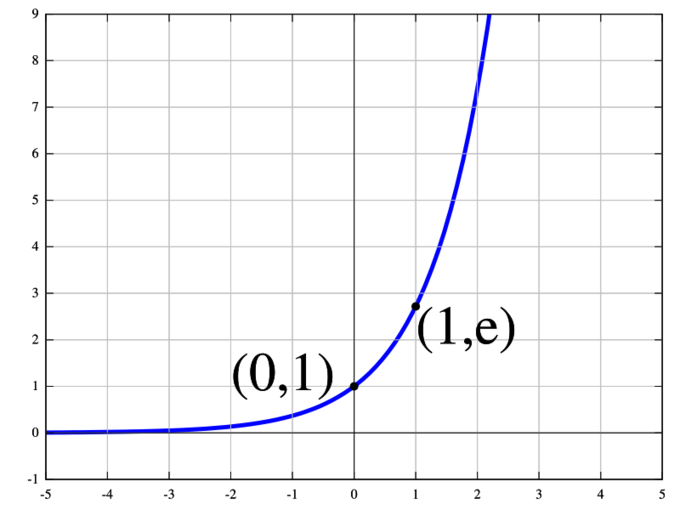
image

Exponential Function: The natural exponential function [latex]y = e^x[/latex].

First, we determine the derivative of [latex]e^{x}[/latex] using the definition of the derivative: [latex-display]\dfrac{d}{dx}e^{x} =\lim_{h \to 0}\dfrac{e^{x + h} - e^{x}}{h}[/latex-display] Then we apply some basic algebra with powers: [latex-display]\dfrac{d}{dx}e^{x} =\lim_{h \to 0}\dfrac{e^{x}e^{h} - e^{x}}{h}[/latex-display] Since [latex]e^{x}[/latex] does not depend on [latex]h[/latex], it is constant as [latex]h[/latex] goes to [latex]0[/latex]. Thus, we can use the limit rules to move it to the outside, leaving us with [latex-display]\dfrac{d}{dx}e^{x} =e^{x}\lim_{h \to 0}\dfrac{e^{h} - 1}{h}[/latex-display] The limit can then be calculated using L'Hôpital's rule: [latex-display]\lim_{h \to 0}\dfrac{e^{h} - 1}{h} = 1[/latex-display] Now we have proven the following rule: [latex-display]\dfrac{d}{dx}e^{x} =e^{x}[/latex-display] Now that we have derived a specific case, let us extend things to the general case of exponential function. Assuming that [latex]a[/latex] is a positive real constant, we wish to calculate the following: [latex-display]\dfrac{d}{dx}a^{x}[/latex-display] Since we have already determined the derivative of [latex]e^{x}[/latex], we will attempt to rewrite [latex]a^{x}[/latex] in that form. Using that [latex]e^{\ln(c)} = c[/latex] and that [latex]\ln(ab) = b \cdot \ln(a)[/latex], we find that: [latex-display]a^{x} = e^{x\cdot \ln(a)}[/latex-display] Now, we simply apply the chain rule: [latex-display]\dfrac{d}{dx}e^{x\cdot \ln(a)} = \dfrac{d}{dx}\left(x\cdot \ln(a)\right)e^{x\cdot \ln(a)} = \ln(a)a^{x}[/latex-display] Derivative of the exponential function: [latex-display]\dfrac{d}{dx}a^x = \ln(a)a^{x}[/latex-display] Here we consider integration of natural exponential function. Note that the exponential function [latex]y = e^{x}[/latex] is defined as the inverse of [latex]\ln(x)[/latex]. Therefore [latex]\ln(e^x) = x[/latex] and [latex]e^{\ln x} = x[/latex]. Let's consider the example of [latex]\int e^{x}dx[/latex]. Since [latex]e^{x} = (e^{x})'[/latex] we can integrate both sides to get: [latex-display]\displaystyle{\int e^{x}dx = e^{x} + C}[/latex-display]

Exponential Growth and Decay

Exponential growth occurs when the growth rate of the value of a mathematical function is proportional to the function's current value.

Learning Objectives

Apply the exponential growth and decay formulas to real world examples

Key Takeaways

Key Points

  • The formula for exponential growth of a variable [latex]x[/latex] at the (positive or negative) growth rate [latex]r[/latex], as time [latex]t[/latex] goes on in discrete intervals (that is, at integer times [latex]0, 1, 2, 3, \cdots[/latex]), is: [latex]x_{t} = x_{0}(1 + r^{t})[/latex] where [latex]x_0[/latex] is the value of [latex]x[/latex] at time [latex]0[/latex].
  • Exponential decay occurs in the same way as exponential growth, providing the growth rate is negative.
  • In the long run, exponential growth of any kind will overtake linear growth of any kind as well as any polynomial growth.

Key Terms

  • exponential: any function that has an exponent as an independent variable
  • linear: having the form of a line; straight
  • polynomial: an expression consisting of a sum of a finite number of terms, each term being the product of a constant coefficient and one or more variables raised to a non-negative integer power
Exponential growth occurs when the growth rate of the value of a mathematical function is proportional to the function's current value. Exponential decay occurs in the same way, providing the growth rate is negative. In the long run, exponential growth of any kind will overtake linear growth of any kind as well as any polynomial growth.
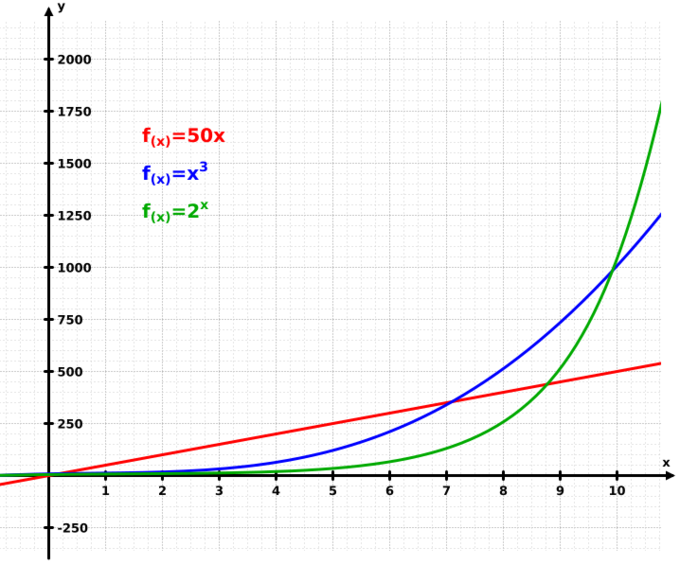
image

Exponential Growth: This graph illustrates how exponential growth (green) surpasses both linear (red) and cubic (blue) growth.

The formula for exponential growth of a variable [latex]x[/latex] at the (positive or negative) growth rate [latex]r[/latex], as time [latex]t[/latex] goes on in discrete intervals (that is, at integer times 0, 1, 2, 3,...), is: [latex-display]x_{t} = x_{0}(1 + r^{t})[/latex-display] where [latex]x_0[/latex] is the value of [latex]x[/latex] at time [latex]0[/latex]. For example, with a growth rate of [latex]r = 5 \% = 0.05[/latex], going from any integer value of time to the next integer causes [latex]x[/latex] at the second time to be [latex]1.05[/latex] times (i.e., [latex]5\%[/latex] larger than) what it was at the previous time. A quantity [latex]x[/latex] depends exponentially on time [latex]b[/latex] if: [latex-display]\displaystyle{x_{t} = ab^{\left(\frac{t}{\tau }\right)}}[/latex-display] where the constant [latex]a[/latex] is the initial value of [latex]x[/latex], [latex]x(0) = a[/latex], the constant [latex]b[/latex] is a positive growth factor, and [latex]\tau[/latex] is the time constant—the time required for [latex]x[/latex] to increase by one factor of [latex]b[/latex]: [latex-display]x(\tau + t)= ab^{\left(\frac{\tau + t}{\tau }\right)} = ab^{\left(\frac{t}{\tau }\right)}b^{\left(\frac{\tau }{\tau}\right)} = x (t)b[/latex-display] If [latex]\tau > 0[/latex] and [latex]b > 1[/latex], then [latex]x[/latex] has exponential growth. If [latex]\tau<0[/latex] and [latex]b > 1[/latex], or [latex]\tau > 0[/latex] and [latex]0 < b < 1[/latex], then [latex]x[/latex] has exponential decay. Let's assume that a species of bacteria doubles every ten minutes. Starting out with only one bacterium, how many bacteria would be present after one hour? The question implies [latex]a=1[/latex], [latex]b=2[/latex], and [latex]\tau = 10\text{ min}[/latex]. [latex-display]x (t) = ab^{\dfrac{t}{\tau}} = 1 \cdot 2^{\left(\frac{60\text{ min}}{10\text{ min}}\right)}[/latex-display] [latex-display]x (1\text{ hour}) = 1 \cdot 2^{(6)} = 64[/latex-display] After one hour, or six ten-minute intervals, there would be sixty-four bacteria.

Inverse Trigonometric Functions: Differentiation and Integration

It is useful to know the derivatives and antiderivatives of the inverse trigonometric functions.

Learning Objectives

Practice integrating and differentiating inverse trigonometric functions

Key Takeaways

Key Points

  • The inverse trigonometric functions "undo" the trigonometric functions [latex]\sin[/latex], [latex]\cos[/latex], and [latex]\tan[/latex].
  • The inverse trigonometric functions are [latex]\arcsin[/latex], [latex]\arccos[/latex], and [latex]\arctan[/latex].
  • Memorizing their derivatives and antiderivatives can be useful.

Key Terms

  • trigonometric: relating to the functions used in trigonometry: [latex]\sin[/latex], [latex]\cos[/latex], [latex]\tan[/latex], [latex]\csc[/latex], [latex]\cot[/latex], [latex]\sec[/latex]
The inverse trigonometric functions are also known as the "arc functions". There are three common notations for inverse trigonometric functions. The arcsine function, for instance, could be written as [latex]\sin^{-1}[/latex], [latex]\text{asin}[/latex], or, as is used on this page, [latex]\arcsin[/latex]. Inverse trigonometric functions include [latex]\arcsin[/latex] and [latex]\arccos[/latex]; [latex]\arctan[/latex] and [latex]\text{arccot}[/latex]; and [latex]\text{arcsec}[/latex] and [latex]\text{arccsc}[/latex]. They can be thought of as the inverses of the corresponding trigonometric functions.
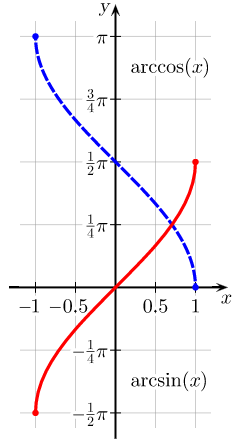
image

Arcsine and Arccosine: The usual principal values of the [latex]\arcsin(x)[/latex] and [latex]\arccos(x)[/latex] functions graphed on the Cartesian plane.

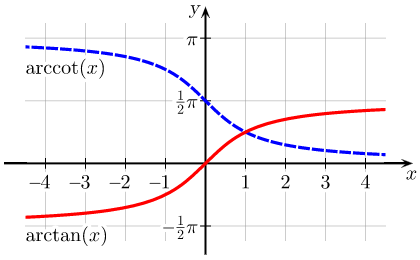
image

Arctangent and Arccotangent: The usual principal values of the [latex]\text{arctan}(x)[/latex] and [latex]\text{arccot}(x)[/latex] functions graphed on the Cartesian plane.

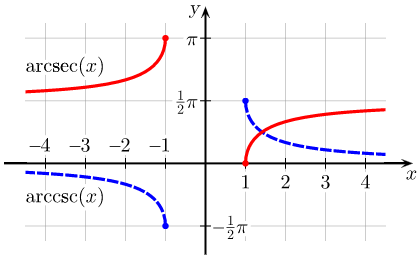
image

Arcsecant and Arccosecant: Principal values of the [latex]\text{arcsec}(x)[/latex] and [latex]\text{arccsc}(x)[/latex] functions graphed on the Cartesian plane.

The differentiation of trigonometric functions is the mathematical process of finding the rate at which a trigonometric function changes with respect to a variable. The integration of trigonometric functions involves finding the antiderivative. The following is a list of indefinite integrals (antiderivatives) of expressions involving the inverse trigonometric functions. [latex-display]\displaystyle{\int \text{arcsec}( a x) dx = x \ \text{arcsec}(a x) - \dfrac{1}{a} \text{arctanh}\left(\sqrt{1-\dfrac{1}{a^2 x^2}} + C\right)}[/latex-display] [latex-display]\displaystyle{\int \text{arccsc}( a x) dx = x \ \text{arccsc}(a x) + \dfrac{1}{a} \text{arctanh}\left(\sqrt{1-\dfrac{1}{a^2 x^2}} + C\right)}[/latex-display] [latex]C[/latex] is used for the arbitrary constant of integration that can only be determined if something about the value of the integral at some point is known. Thus each function has an infinite number of antiderivatives. The derivatives of the inverse trigonometric functions are as follows: [latex-display]\dfrac{d}{dx} \text{arccot}(x) = \dfrac {-1} {1 + x^2}[/latex-display] [latex-display]\dfrac{d}{dx} \text{arcsec}(x) = \dfrac {1} {x^2\sqrt{1 - x^{-2}}}[/latex-display] [latex-display]\dfrac{d}{dx} \text{arccsc}(x) = \dfrac {-1} {x^2\sqrt{1 - x^{-2}}}[/latex-display] Note that some of these functions are not valid for a range of [latex]x[/latex] which would end up making the function undefined.

Hyperbolic Functions

[latex]\sinh[/latex] and [latex]\cosh[/latex] are basic hyperbolic functions; [latex]\sinh[/latex] is defined as the following: [latex]\sinh (x) = \frac{e^x - e^{-x}}{2}[/latex].

Learning Objectives

Discuss the basic properties of hyperbolic functions

Key Takeaways

Key Points

  • The basic hyperbolic functions are the hyperbolic sine "[latex]\sinh[/latex]," and the hyperbolic cosine "[latex]\cosh[/latex]," from which are derived the hyperbolic tangent "[latex]\tanh[/latex]," and so on, corresponding to the derived trigonometric functions.
  • The inverse hyperbolic functions are the area hyperbolic sine "[latex]\text{arsinh}[/latex]" (also called "[latex]\text{asinh}[/latex]" or sometimes "[latex]\text{arcsinh}[/latex]") and so on.
  • The hyperbolic functions take real values for a real argument called a hyperbolic angle. The size of a hyperbolic angle is the area of its hyperbolic sector.

Key Terms

  • meromorphic: relating to or being a function of a complex variable that is analytic everywhere in a region except for singularities at each of which infinity is the limit and each of which is contained in a neighborhood where the function is analytic except for the singular point itself
  • inverse: a function that undoes another function
Hyperbolic function is an analog of the ordinary trigonometric function, also called circular function. The basic hyperbolic functions are the hyperbolic sine "[latex]\sinh[/latex]," and the hyperbolic cosine "[latex]\cosh[/latex]," from which are derived the hyperbolic tangent "[latex]\tanh[/latex]," and so on, corresponding to the derived functions. The inverse hyperbolic functions are the area hyperbolic sine "arsinh" (also called "asinh" or sometimes "arcsinh") and so on. Just as the points ([latex]\cos t[/latex], [latex]\sin t[/latex]) form a circle with a unit radius, the points ([latex]\cosh t[/latex], [latex]\sinh t[/latex]) form the right half of the equilateral hyperbola. Hyperbolic functions occur in the solutions of some important linear differential equations, for example the equation defining a catenary, of some cubic equations, and of Laplace's equation in Cartesian coordinates. The latter is important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity. The hyperbolic functions take real values for a real argument called a hyperbolic angle. The size of a hyperbolic angle is the area of its hyperbolic sector. The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector. In complex analysis, the hyperbolic functions arise as the imaginary parts of sine and cosine. When considered defined by a complex variable, the hyperbolic functions are rational functions of exponentials, and are hence meromorphic. The hyperbolic functions are as follows.

Hyperbolic sine

[latex-display]\sinh (x) = \dfrac{e^x - e^{-x}}{2}[/latex-display]

Hyperbolic cosine

[latex-display]\cosh (x) =\dfrac{e^x + e^{-x}}{2}[/latex-display]

Hyperbolic tangent

[latex-display]\tanh (x) = \dfrac{\sinh(x)}{\cosh (x)} = \dfrac{1 - e^{-2x}}{1 + e^{-2x}}[/latex-display]

Hyperbolic cotangent

[latex-display]\coth (x) = \dfrac{\cosh (x)}{\sinh (x)} = \dfrac{1 + e^{-2x}}{1 - e^{-2x}}[/latex-display]

Hyperbolic secant

[latex-display]\text{sech} (x) = (\cosh (x))^{-1}= \dfrac{2}{e^x + e^{-x}}[/latex-display]

Hyperbolic cosecant

[latex-display]\text{csch} (x)= (\sinh (x))^{-1}= \dfrac{2}{e^x - e^{-x}}[/latex-display]

Indeterminate Forms and L'Hôpital's Rule

Indeterminate forms like [latex]\frac{0}{0}[/latex] have no definite value; however, when a limit is indeterminate, l'Hôpital's rule can often be used to evaluate it.

Learning Objectives

Use L'Hopital's Rule to evaluate limits involving indeterminate forms

Key Takeaways

Key Points

  • Indeterminate forms include [latex]0^0[/latex], [latex]\frac{0}{0}[/latex], [latex]1^\infty[/latex], [latex]\infty - \infty[/latex], [latex]\frac{\infty}{\infty}[/latex], [latex]0 \times \infty[/latex], and [latex]\infty^0[/latex]
  • Indeterminate forms often arise when you are asked to take the limit of a function. For example: [latex]\lim_{x\to 0}\frac{x}{x}[/latex] is indeterminate, giving [latex]\frac{0}{0}[/latex].
  • L'Hôpital's rule: For [latex]f[/latex] and [latex]g[/latex] which are differentiable, if [latex]\lim_{x\to c}f(x)=\lim_{x \to c}g(x) = 0[/latex] or [latex]\pm \infty[/latex] and [latex]\lim_{x\to c}\frac{f'(x)}{g'(x)}[/latex] exists, and [latex]g'(x) \neq 0[/latex] for all [latex]x[/latex] in the interval containing [latex]c[/latex], then [latex]\lim_{x \to c}\frac{f(x)}{g(x)} = \lim_{x\to c}\frac{f'(x)}{g'(x)}[/latex].

Key Terms

  • limit: a value to which a sequence or function converges
  • differentiable: a function that has a defined derivative (slope) at each point
  • indeterminate: not accurately determined or determinable
Occasionally in mathematics, one runs across an equation with an indeterminate form as seen in. In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is known as an indeterminate form. The indeterminate forms include [latex]0^0[/latex], [latex]\frac{0}{0}[/latex], [latex]1^\infty[/latex], [latex]\infty - \infty[/latex], [latex]\frac{\infty}{\infty}[/latex], [latex]0 \times \infty[/latex], and [latex]\infty^0[/latex]. The most common example of an indeterminate form is [latex]\frac{0}{0}[/latex]. As [latex]x[/latex] approaches [latex]0[/latex], the ratios [latex]\frac{x}{x^3}[/latex], [latex]\frac{x}{x}[/latex], and [latex]\frac{x^2}{x}[/latex] go to [latex]\infty[/latex], [latex]1[/latex], and [latex]0[/latex], respectively. In each case, however, if the limits of the numerator and denominator are evaluated and plugged into the division operation, the resulting expression is [latex]\frac{0}{0}[/latex]. So, roughly speaking, [latex]\frac{0}{0}[/latex] can be [latex]0[/latex], or [latex]\infty[/latex], or it can be [latex]1[/latex]—in fact, it is possible to construct similar examples converging to any particular value. That is why the expression [latex]\frac{0}{0}[/latex] is indeterminate. More formally, the fact that the functions [latex]f[/latex] and [latex]g[/latex] both approach [latex]0[/latex] as [latex]x[/latex] approaches some limit point [latex]c[/latex] is not enough information to evaluate the limit [latex]\lim_{x\to c}\frac{f(x)}{g(x)}[/latex]. That limit could converge to any number, or diverge to infinity, or might not exist, depending on what the functions [latex]f[/latex] and [latex]g[/latex] are. For example, [latex]\lim_{x\to 0}\frac{x}{x}[/latex] is indeterminate.

L'Hôpital's Rule

In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application (or repeated application) of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit. In its simplest form, l'Hôpital's rule states that for functions [latex]f[/latex] and [latex]g[/latex] which are differentiable, if [latex-display]\displaystyle{\lim_{x\to c}f(x)=\lim_{x \to c}g(x) = 0 \text{ or } \pm \infty}[/latex-display] and [latex]\lim_{x\to c}\frac{f'(x)}{g'(x)}[/latex] exists, and [latex]g'(x) \neq 0[/latex] for all [latex]x[/latex] in the interval containing [latex]c[/latex], then: [latex-display]\displaystyle{\lim_{x \to c}\frac{f(x)}{g(x)} = \lim_{x\to c}\frac{f'(x)}{g'(x)}}[/latex-display]

Bases Other than e and their Applications

Among all choices for the base [latex]b[/latex], particularly common values for logarithms are [latex]e[/latex], [latex]2[/latex], and [latex]10[/latex].

Learning Objectives

Distinguish between the different applications for logarithms in various bases

Key Takeaways

Key Points

  • The major advantage of common logarithms (logarithms to base ten) is that they are easy to use for manual calculations in the decimal number system.
  • The binary logarithm is often used in computer science and information theory because it is closely connected to the binary numeral system.
  • Common logarithm is frequently written as "[latex]\log(x)[/latex]"; binary logarithm is frequently written "[latex]\text{ld}\, n[/latex]" or "[latex]\lg n[/latex]".

Key Terms

  • logarithm: the exponent by which another fixed value, the base, must be raised to produce that number
Among all choices for the base [latex]b[/latex], three are particularly common for logarithms. These are [latex]b = 10[/latex] (common logarithm); [latex]b = e[/latex] ( natural logarithm ), and [latex]b = 2[/latex] (binary logarithm). In this atom we will focus on common and binary logarithms. The major advantage of common logarithms (logarithms in base ten) is that they are easy to use for manual calculations in the decimal number system: [latex-display]\log_{10}(10x) = \log_{10}(10)+ \log_{10}(x) = 1 + \log_{10}(x)[/latex-display] Thus, [latex]\log_{10}(x)[/latex] is related to the number of decimal digits of a positive integer [latex]x[/latex]: the number of digits is the smallest integer strictly bigger than [latex]\log_{10}(x)[/latex]. For example, [latex]\log_{10}(1430)[/latex] is approximately [latex]3.15[/latex]. The next integer is [latex]4[/latex], which is the number of digits of [latex]1430[/latex]. Before the early 1970s, hand-held electronic calculators were not yet in widespread use. Due to their utility in saving work in laborious multiplications and divisions with pen and paper, tables of base-ten logarithms were given in appendices of many books. Such a table of "common logarithms" gave the logarithm—often to four or five decimal places—of each number in the left-hand column, which ran from [latex]1[/latex] to [latex]10[/latex] by small increments, perhaps [latex]0.01[/latex] or [latex]0.001[/latex]. There was only a need to include numbers between [latex]1[/latex] and [latex]10[/latex], since the logarithms of larger numbers were easily calculated. Because base-ten logarithms were most useful for computations, engineers generally wrote [latex]\log(x)[/latex] when they meant [latex]\log_{10}(x)[/latex]. Mathematicians, on the other hand, wrote [latex]\log(x)[/latex] when they meant [latex]\log_e(x)[/latex] for the natural logarithm. Today, both notations are found. Since hand-held electronic calculators are designed by engineers rather than mathematicians, they customarily follow engineers' notation. Binary logarithm ([latex]\log _2 n[/latex]) is the logarithm in base [latex]2[/latex]. It is the inverse function of [latex]n \Rightarrow 2^n[/latex]. The binary logarithm of [latex]n[/latex] is the power to which the number [latex]2[/latex] must be raised to obtain the value [latex]n[/latex]. This makes the binary logarithm useful for anything involving powers of [latex]2[/latex] (i. e., doubling). For example, the binary logarithm of [latex]1[/latex] is [latex]0[/latex], the binary logarithm of [latex]2[/latex] is 1, the binary logarithm of [latex]4[/latex] is [latex]2[/latex], the binary logarithm of [latex]8[/latex] is [latex]3[/latex], the binary logarithm of [latex]16[/latex] is [latex]4[/latex], and the binary logarithm of [latex]32[/latex] is [latex]5[/latex]. The binary logarithm is often used in computer science and information theory because it is closely connected to the binary numeral system. It is frequently written as "[latex]\text{ld}\, n[/latex]" or "[latex]\lg n[/latex]".

Licenses & Attributions

CC licensed content, Shared previously

CC licensed content, Specific attribution