We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Boundless Calculus

Infinite Sequences and Series

Sequences

A sequence is an ordered list of objects and can be considered as a function whose domain is the natural numbers.

Learning Objectives

Distinguish a sequence and a set

Key Takeaways

Key Points

  • Like a set, a sequence contains members (also called elements). Unlike a set, order matters in a sequence, and the same elements can appear multiple times at different positions.
  • The terms of a sequence are commonly denoted by a single variable, say [latex]a_n[/latex], where the index [latex]n[/latex] indicates the [latex]n[/latex]th element of the sequence.
  • Sequences whose elements are related to the previous elements in a straightforward way are often specified using recursion.

Key Terms

  • set: a collection of distinct objects, considered as an object in its own right
  • recursion: the act of defining an object (usually a function) in terms of that object itself
A sequence is an ordered list of objects (or events). Like a set, it contains members (also called elements, or terms). The number of ordered elements (possibly infinite) is called the length of the sequence. Unlike a set, order matters in a sequence, and exactly the same elements can appear multiple times at different positions in the sequence. Most precisely, a sequence can be defined as a function whose domain is a countable, totally ordered set, such as the natural numbers. Examples: [latex](M, A, R, Y)[/latex] is a different sequence from [latex](A, R, M, Y)[/latex]. Also, the sequence [latex](1, 1, 2, 3, 5, 8)[/latex], which contains the number [latex]1[/latex] at two different positions, is a valid sequence. Sequences can be finite, as in this example, or infinite, such as the sequence of all even positive integers [latex](2, 4, 6, \cdots)[/latex]. Finite sequences are sometimes known as strings or words, and infinite sequences as streams. The empty sequence [latex]( \quad )[/latex] is included in most notions of sequence, but may be excluded depending on the context.

Indexing

The terms of a sequence are commonly denoted by a single variable, say [latex]a_n[/latex], where the index [latex]n[/latex] indicates the [latex]n[/latex]th element of the sequence. Indexing notation is used to refer to a sequence in the abstract. It is also a natural notation for sequences whose elements are related to the index [latex]n[/latex] (the element's position) in a simple way. For instance, the sequence of the first 10 square numbers could be written as: [latex-display](a_1,a_2, \cdots,a_{10}), \quad a_k = k^2[/latex-display] This represents the sequence [latex](1,4,9, \cdots, 100)[/latex]. Sequences can be indexed beginning and ending from any integer. The infinity symbol, [latex]\infty[/latex], is often used as the superscript to represent the sequence that includes all integer [latex]k[/latex]-values starting with a certain one. The sequence of all positive squares is then denoted as: [latex]\displaystyle{(a_k)_{k=1}^\infty, \quad a_k = k^2}[/latex].
image

A Convergent Sequence: The plot of a convergent sequence ([latex]a_n[/latex]) is shown in blue. Visually, we can see that the sequence is converging to the limit of [latex]0[/latex] as [latex]n[/latex] increases.

Specifying a Sequence by Recursion

Sequences whose elements are related to the previous elements in a straightforward way are often specified using recursion. This is in contrast to the specification of sequence elements in terms of their position. To specify a sequence by recursion requires a rule to construct each consecutive element in terms of the ones before it. In addition, enough initial elements must be specified so that new elements of the sequence can be specified by the rule.

Example

The Fibonacci sequence can be defined using a recursive rule along with two initial elements. The rule is that each element is the sum of the previous two elements, and the first two elements are [latex]0[/latex] and [latex]1[/latex]: [latex]a_n = a_{n-1} + a_{n-2}[/latex] and [latex]a_0 = 0, \, a_1=1[/latex]. The first ten terms of this sequence are ([latex]0,1,1,2,3,5,8,13,21,34[/latex]).

Series

A series is the sum of the terms of a sequence.

Learning Objectives

State the requirements for a series to converge to a limit

Key Takeaways

Key Points

  • Given an infinite sequence of numbers [latex]\{ a_n \}[/latex], a series is informally the result of adding all those terms together: [latex]\sum_{n=0}^\infty a_n[/latex].
  • Unlike finite summations, infinite series need tools from mathematical analysis, specifically the notion of limits, to be fully understood and manipulated.
  • By definition, a series converges to a limit [latex]L[/latex] if and only if the associated sequence of partial sums converges to [latex]L[/latex]: [latex]L = \sum_{n=0}^{\infty}a_n \Leftrightarrow L = \lim_{k \rightarrow \infty} S_k[/latex].

Key Terms

  • sequence: an ordered list of objects
  • Zeno's dichotomy: That which is in locomotion must arrive at the half-way stage before it arrives at the goal.
A series is, informally speaking, the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely. Given an infinite sequence of numbers [latex]\{ a_n \}[/latex], a series is informally the result of adding all those terms together: [latex]a_1 + a_2 + a_3 + \cdots[/latex]. These can be written more compactly using the summation symbol [latex]\Sigma[/latex]. An example is the famous series from Zeno's dichotomy and its mathematical representation: [latex-display]\displaystyle{\sum_{n=1}^\infty \frac{1}{2^n} = \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+\cdots}[/latex-display]
image

Zeno's Paradox: Say you are working from a location [latex]x=0[/latex] toward [latex]x=100[/latex]. Before you can get there, you must get halfway there. Before you can get halfway there, you must get a quarter of the way there. Before traveling a quarter, you must travel one-eighth; before an eighth, one-sixteenth; and so on.

The terms of the series are often produced according to a certain rule, such as by a formula or by an algorithm. As there are an infinite number of terms, this notion is often called an infinite series. Unlike finite summations, infinite series need tools from mathematical analysis, specifically the notion of limits, to be fully understood and manipulated. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, and finance.

Definition

For any sequence of rational numbers, real numbers, complex numbers, functions thereof, etc., the associated series is defined as the ordered formal sum: [latex-display]\displaystyle{\sum_{n=0}^{\infty}a_n = a_0 + a_1 + a_2 + \cdots}[/latex-display] The sequence of partial sums [latex]\{S_k\}[/latex] associated to a series [latex]\sum_{n=0}^\infty a_n[/latex] is defined for each k as the sum of the sequence [latex]\{a_n\}[/latex] from [latex]a_0[/latex] to [latex]a_k[/latex]: [latex-display]\displaystyle{S_k = \sum_{n=0}^{k}a_n = a_0 + a_1 + \cdots + a_k}[/latex-display] By definition, the series [latex]\sum_{n=0}^{\infty} a_n[/latex] converges to a limit [latex]L[/latex] if and only if the associated sequence of partial sums [latex]\{S_k\}[/latex] converges to [latex]L[/latex]. This definition is usually written as follows: [latex-display]\displaystyle{L = \sum_{n=0}^{\infty}a_n \Leftrightarrow L = \lim_{k \rightarrow \infty} S_k}[/latex-display]

The Integral Test and Estimates of Sums

The integral test is a method of testing infinite series of nonnegative terms for convergence by comparing them to an improper integral.

Learning Objectives

Describe the purpose of the integral test

Key Takeaways

Key Points

  • The integral test uses a monotonically decreasing function [latex]f[/latex] defined on the unbounded interval [latex][N, \infty)[/latex] (where [latex]N[/latex] is an integer).
  • The infinite series [latex]\sum_{n=N}^\infty f(n)[/latex] converges to a real number if and only if the improper integral [latex]\int_N^\infty f(x)\,dx[/latex] is finite. In other words, if the integral diverges, then the series diverges as well.
  • Integral tests proves that the harmonic series [latex]\sum_{n=1}^\infty \frac1n[/latex] diverges.

Key Terms

  • improper integral: an integral where at least one of the endpoints is taken as a limit, either to a specific number or to infinity
  • natural logarithm: the logarithm in base [latex]e[/latex]
The integral test for convergence is a method used to test infinite series of non-negative terms for convergence. It was developed by Colin Maclaurin and Augustin-Louis Cauchy and is sometimes known as the Maclaurin–Cauchy test.

Statement of the test

Consider an integer [latex]N[/latex] and a non-negative function [latex]f[/latex] defined on the unbounded interval [latex][N, \infty )[/latex], on which it is monotonically decreasing. The infinite series [latex]\sum_{n=N}^\infty f(n)[/latex] converges to a real number if and only if the improper integral [latex]\int_N^\infty f(x)\,dx[/latex] is finite. In other words, if the integral diverges, then the series diverges as well. Although we won't go into the details, the proof of the test also gives the lower and upper bounds: [latex-display]\displaystyle{\int_N^\infty f(x)\,dx\le\sum_{n=N}^\infty f(n)\le f(N)+\int_N^\infty f(x)\,dx}[/latex-display] for the infinite series.

Applications

The harmonic series [latex]\sum_{n=1}^\infty \frac1n[/latex] diverges because, using the natural logarithm (its derivative) and the fundamental theorem of calculus, we get: [latex-display]\displaystyle{\int_1^M\frac1x\,dx=\ln x\Bigr|_1^M=\ln M\to\infty \quad\text{for }M\to\infty}[/latex-display] On the other hand, the series [latex]\sum_{n=1}^\infty \frac1{n^{1+\varepsilon}}[/latex] converges for every [latex]\varepsilon > 0[/latex] because, by the power rule: [latex-display]\displaystyle{\int_1^M\frac1{x^{1+\varepsilon}}\,dx =-\frac1{\varepsilon x^\varepsilon}\biggr|_1^M= \frac1\varepsilon\Bigl(1-\frac1{M^\varepsilon}\Bigr) \le\frac1\varepsilon }[/latex-display]
image

Integral Test: The integral test applied to the harmonic series. Since the area under the curve [latex]y = \frac{1}{x}[/latex] for [latex]x \in [1, \infty)[/latex] is infinite, the total area of the rectangles must be infinite as well.

The above examples involving the harmonic series raise the question of whether there are monotone sequences such that [latex]f(n)[/latex] decreases to [latex]0[/latex] faster than [latex]\frac{1}{n}[/latex]but slower than [latex]\frac{1}{n^{1 + \varepsilon}}[/latex] in the sense that: [latex-display]\displaystyle{\lim_{n\to\infty}\frac{f(n)}{\frac{1}{n}}=0}[/latex-display] and: [latex-display]\displaystyle{\lim_{n\to\infty}\frac{f(n)}{\frac{1}{n^{1+\varepsilon}}}=\infty}[/latex-display] for every [latex]\varepsilon > 0[/latex], and whether the corresponding series of the [latex]f(n)[/latex] still diverges. Once such a sequence is found, a similar question can be asked of [latex]f(n)[/latex] taking the role of [latex]\frac{1}{n}[/latex] oand so on. In this way, it is possible to investigate the borderline between divergence and convergence of infinite series.

Comparison Tests

Comparison test may mean either limit comparison test or direct comparison test, both of which can be used to test convergence of a series.

Learning Objectives

Distinguish the limit comparison and the direct comparison tests

Key Takeaways

Key Points

  • For sequences [latex]\{a_n \}[/latex], [latex]\{b_n \}[/latex], both with non-negative terms only, if [latex]\lim_{n \to \infty} \frac{a_n}{b_n} = c[/latex] with [latex]0 < c < \infty[/latex].
  • If the infinite series [latex]\sum b_n[/latex] converges and [latex]0 \le a_n \le b_n[/latex] for all sufficiently large [latex]n[/latex] (that is, for all [latex]n > N[/latex] for some fixed value [latex]N[/latex]), then the infinite series [latex]\sum a_n[/latex] also converges.
  • If the infinite series [latex]\sum b_n[/latex] diverges and [latex]0 \le a_n \le b_n[/latex] for all sufficiently large [latex]n[/latex], then the infinite series [latex]\sum a_n[/latex] also diverges.

Key Terms

  • integral test: a method used to test infinite series of non-negative terms for convergence by comparing it to improper integrals
  • improper integral: an integral where at least one of the endpoints is taken as a limit, either to a specific number or to infinity
Comparison tests may mean either limit comparison tests or direct comparison tests. The limit comparison test is a method of testing for the convergence of an infinite series, while the direct comparison test is a way of deducing the convergence or divergence of an infinite series or an improper integral by comparison with other series or integral whose convergence properties are already known.

Limit Comparison Test

Statement: Suppose that we have two series, [latex]\Sigma_n a_n[/latex] and [latex]\Sigma_n b_n[/latex], where [latex]a_n[/latex], [latex]b_n[/latex] are greater than or equal to [latex]0[/latex] for all [latex]n[/latex]. If [latex]\lim_{n \to \infty} \frac{a_n}{b_n} = c[/latex] with [latex]0 < c < \infty[/latex], then either both series converge or both series diverge. Example: We want to determine if the series [latex]\Sigma \frac{n+1}{2n^2}[/latex] converges or diverges. For this we compare it with the series [latex]\Sigma \frac{1}{n}[/latex], which diverges. As [latex]\lim_{n \to \infty} \frac{n+1}{2n^2} \frac{n}{1} = \frac{1}{2}[/latex], we have that the original series also diverges.
image

Limit Convergence Test: The ratio between [latex]\frac{n+1}{2n^2}[/latex] and [latex]\frac{1}{n}[/latex] for [latex]n \rightarrow ∞[/latex] is [latex]\frac{1}{2}[/latex]. Since the sum of the sequence [latex]\frac{1}{n}[/latex] [latex]\left ( \text{i.e., }\sum {\frac{1}{n}}\right)[/latex] diverges, the limit convergence test tells that the original series (with [latex]\frac{n+1}{2n^2}[/latex]) also diverges.

Direct Comparison Test

The direct comparison test provides a way of deducing the convergence or divergence of an infinite series or an improper integral. In both cases, the test works by comparing the given series or integral to one whose convergence properties are known. In this atom, we will check the series case only. For sequences [latex]\{a_n\}[/latex], [latex]\{b_n\}[/latex] with non-negative terms:
  • If the infinite series [latex]\sum b_n[/latex] converges and [latex]0 \le a_n \le b_n[/latex] for all sufficiently large [latex]n[/latex] (that is, for all [latex]n>N[/latex] for some fixed value [latex]N[/latex]), then the infinite series [latex]\sum a_n[/latex] also converges.
  • If the infinite series [latex]\sum b_n[/latex] diverges and [latex]a_n \ge b_n \ge 0[/latex] for all sufficiently large [latex]n[/latex], then the infinite series [latex]\sum a_n[/latex] also diverges.

Example

The series [latex]\Sigma \frac{1}{n^3 + 2n}[/latex] converges because [latex]\frac{1}{n^3 + 2n} < \frac{1}{n^3}[/latex] for [latex]n > 0[/latex] and [latex]\Sigma \frac{1}{n^3}[/latex] converges.

Alternating Series

An alternating series is an infinite series of the form [latex]\sum_{n=0}^\infty (-1)^n\,a_n[/latex] or [latex]\sum_{n=0}^\infty (-1)^{n-1}\,a_n[/latex] with [latex]a_n > 0[/latex] for all [latex]n[/latex].

Learning Objectives

Describe the properties of an alternating series and the requirements for one to converge

Key Takeaways

Key Points

  • The theorem known as the "Leibniz Test," or the alternating series test, tells us that an alternating series will converge if the terms [latex]a_n[/latex] converge to [latex]0[/latex] monotonically.
  • The signs of the general terms alternate between positive and negative.
  • The sum [latex]\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}[/latex] converges by the alternating series test.

Key Terms

  • monotone: property of a function to be either always decreasing or always increasing
  • Cauchy sequence: a sequence whose elements become arbitrarily close to each other as the sequence progresses
An alternating series is an infinite series of the form: [latex-display]\displaystyle{\sum_{n=0}^\infty (-1)^n\,a_n}[/latex-display] or: [latex-display]\displaystyle{\sum_{n=0}^\infty (-1)^{n-1}\,a_n}[/latex-display] with [latex]a_n > 0[/latex] for all [latex]n[/latex]. The signs of the general terms alternate between positive and negative. Like any series, an alternating series converges if and only if the associated sequence of partial sums converges.

Alternating Series Test

The theorem known as the "Leibniz Test," or the alternating series test, tells us that an alternating series will converge if the terms [latex]a_n[/latex] converge to [latex]0[/latex] monotonically. Proof: Suppose the sequence [latex]a_n[/latex] converges to [latex]0[/latex] and is monotone decreasing. If [latex]m[/latex] is odd and [latex]S_m - S_n < a_{m}[/latex] via the following calculation: [latex-display]\begin{align} S_m - S_n & = \sum_{k=0}^m(-1)^k\,a_k\,-\,\sum_{k=0}^n\,(-1)^k\,a_k\ \\& = \sum_{k=m+1}^n\,(-1)^k\,a_k \\ & =a_{m+1}-a_{m+2}+a_{m+3}-a_{m+4}+\cdots+a_n\\ & =\displaystyle a_{m+1}-(a_{m+2}-a_{m+3}) -\cdots-a_n \le a_{m+1}\le a_{m} \\& \quad [a_{n} \text{ decreasing}]. \end{align}[/latex-display] Since [latex]a_n[/latex] is monotonically decreasing, the terms are negative. Thus, we have the final inequality [latex]S_m - S_n \le a_{m}[/latex]. Similarly, it can be shown that, since [latex]a_m[/latex] converges to [latex]0[/latex], [latex]S_m - S_n[/latex] converges to [latex]0[/latex] for [latex]m, n \rightarrow \infty[/latex]. Therefore, our partial sum [latex]S_m[/latex] converges. (The sequence [latex]\{ S_m \}[/latex] is said to form a Cauchy sequence, meaning that elements of the sequence become arbitrarily close to each other as the sequence progresses.) The argument for [latex]m[/latex] even is similar. Example: [latex-display]\displaystyle{\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots}[/latex-display] [latex]a_n = \frac1n[/latex] converges to 0 monotonically. Therefore, the sum [latex]\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}[/latex] converges by the alternating series test.
image

Alternating Harmonic Series: The first fourteen partial sums of the alternating harmonic series (black line segments) shown converging to the natural logarithm of 2 (red line).

Absolute Convergence and Ratio and Root Tests

An infinite series of numbers is said to converge absolutely if the sum of the absolute value of the summand is finite.

Learning Objectives

State the conditions when an infinite series of numbers converge absolutely

Key Takeaways

Key Points

  • A real or complex series [latex]\textstyle\sum_{n=0}^\infty a_n[/latex] is said to converge absolutely if [latex]\textstyle\sum_{n=0}^\infty \left|a_n\right| = L[/latex] for some real number [latex]L[/latex].
  • The root test is a convergence test of an infinite series that makes use of the limit [latex]L = \lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|[/latex].
  • The root test is a criterion for the convergence of an infinite series using the limit superior [latex]C = \limsup_{n\rightarrow\infty}\sqrt[n]{|a_n|}[/latex].

Key Terms

  • summand: something which is added or summed
  • improper integral: an integral where at least one of the endpoints is taken as a limit, either to a specific number or to infinity
  • limit superior: the supremum of the set of accumulation points of a given sequence or set
An infinite series of numbers is said to converge absolutely (or to be absolutely convergent) if the sum of the absolute value of the summand is finite. More precisely, a real or complex series [latex]\textstyle\sum_{n=0}^\infty a_n[/latex] is said to converge absolutely if [latex]\textstyle\sum_{n=0}^\infty \left|a_n\right| = L[/latex] for some real number [latex]L[/latex]. Similarly, an improper integral of a function, [latex]\textstyle\int_0^\infty f(x)\,dx[/latex], is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if [latex]\int_0^\infty \left|f(x)\right|dx = L[/latex]. Absolute convergence is important for the study of infinite series because its definition is strong enough to have properties of finite sums that not all convergent series possess, yet is broad enough to occur commonly. (A convergent series that is not absolutely convergent is called conditionally convergent.)

Ratio Test

The ratio test is a test (or "criterion") for the convergence of a series [latex]\sum_{n=1}^\infty a_n[/latex], where each term is a real or complex number and [latex]a_n[/latex] is nonzero when n is large. The test was first published by Jean le Rond d'Alembert and is sometimes known as d'Alembert's ratio test. The usual form of the test makes use of the limit, [latex]L = \lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|[/latex]. The ratio test states that,
  • if [latex]L < 1[/latex], then the series converges absolutely;
  • if [latex]L > 1[/latex], then the series does not converge;
  • if [latex]L = 1[/latex] or the limit fails to exist, then the test is inconclusive, because there exist both convergent and divergent series that satisfy this case.

Root Test

The root test is a criterion for the convergence (a convergence test) of an infinite series. It depends on the quantity [latex]\limsup_{n\rightarrow\infty}\sqrt[n]{|a_n|}[/latex], where [latex]a_n[/latex] are the terms of the series, and states that the series converges absolutely if this quantity is less than one but diverges if it is greater than one. It is particularly useful in connection with power series. The root test was developed first by Augustin-Louis Cauchy and so is sometimes known as the Cauchy root test, or Cauchy's radical test. For a series [latex]\sum_{n=1}^\infty a_n[/latex], the root test uses the number [latex]C = \limsup_{n\rightarrow\infty}\sqrt[n]{ \left|a_n \right|}[/latex], where "lim sup" denotes the limit superior, possibly ∞. Note that if [latex]\lim_{n\rightarrow\infty}\sqrt[n]{ \left|a_n \right|}[/latex] converges, then it equals [latex]C[/latex] and may be used in the root test instead. The root test states that
  • if [latex]C < 1[/latex], then the series converges absolutely;
  • if [latex]C > 1[/latex], then the series diverges;
  • if [latex]C = 1[/latex] and the limit approaches strictly from above, then the series diverges;
  • otherwise the test is inconclusive (the series may diverge, converge absolutely, or converge conditionally).
There are some series for which [latex]C = 1[/latex] and the series converges, e.g.: [latex-display]\displaystyle{\sum{\frac{1}{n^2}}}[/latex-display] and there are others for which [latex]C = 1[/latex] and the series diverges, e.g.: [latex-display]\displaystyle{\sum{\frac{1}{n}}}[/latex-display]
image

Ratio Test: In this example, the ratio of adjacent terms in the blue sequence converges to [latex]L=\frac{1}{2}[/latex]. We choose [latex]r = \frac{L+1}{2} = \frac{3}{4}[/latex]. Then the blue sequence is dominated by the red sequence for all [latex]n \geq 2[/latex]. The red sequence converges, so the blue sequence does as well.

Tips for Testing Series

Convergence tests are methods of testing for the convergence or divergence of an infinite series.

Learning Objectives

Formulate three techniques that will help when testing the convergence of a series

Key Takeaways

Key Points

  • There is no single convergence test which works for all series out there.
  • Practice and training will help you choose the right test for a given series.
  • We have learned about the root /ratio test, integral test, and direct/ limit comparison test.

Key Terms

  • conditional convergence: A series or integral is said to be conditionally convergent if it converges but does not converge absolutely.
Convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence, or divergence of an infinite series. When testing the convergence of a series, you should remember that there is no single convergence test which works for all series. It is up to you to guess and pick the right test for a given series. Practice and training will help you in expediting this "guessing" process. Here is a summary for the convergence test that we have learned:

List of Tests

Limit of the Summand: If the limit of the summand is undefined or nonzero, then the series must diverge. Ratio test: For [latex]r = \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right|[/latex], if [latex]r < 1[/latex], the series converges; if [latex]r > 1[/latex], the series diverges; if [latex]r = 1[/latex], the test is inconclusive. Root test: For [latex]r = \limsup_{n \to \infty}\sqrt[n]{ \left|a_n \right|}[/latex], if [latex]r < 1[/latex], then the series converges; if [latex]r > 1[/latex], then the series diverges; if [latex]r = 1[/latex], the root test is inconclusive. Integral test: For a positive, monotone decreasing function [latex]f(x)[/latex] such that [latex]f(n)=a_n[/latex], if [latex]\int_{1}^{\infty} f(x)\, dx = \lim_{t \to \infty} \int_{1}^{t} f(x)\, dx < \infty[/latex] then the series converges. But if the integral diverges, then the series does so as well.
image

Integral Test: The integral test applied to the harmonic series. Since the area under the curve [latex]y = \frac{1}{x}[/latex] for [latex]x \in [1, ∞)[/latex] is infinite, the total area of the rectangles must be infinite as well.

Direct comparison test: If the series [latex]\sum_{n=1}^\infty b_n[/latex] is an absolutely convergent series and [latex]\left |a_n \right | \le \left | b_n \right|[/latex] for sufficiently large [latex]n[/latex], then the series [latex]\sum_{n=1}^\infty a_n[/latex] converges absolutely. Limit comparison test: If [latex]\left \{ a_n \right \}, \left \{ b_n \right \} > 0[/latex], and [latex]\lim_{n \to \infty} \frac{a_n}{b_n}[/latex] exists and is not zero, then [latex]\sum_{n=1}^\infty a_n[/latex] converges if and only [latex]if \sum_{n=1}^\infty b_n[/latex] converges.

Power Series

A power series (in one variable) is an infinite series of the form [latex]f(x) = \sum_{n=0}^\infty a_n \left( x-c \right)^n[/latex], where [latex]a_n[/latex] is the coefficient of the [latex]n[/latex]th term and [latex]x[/latex] varies around [latex]c[/latex].

Learning Objectives

Express a power series in a general form

Key Takeaways

Key Points

  • Power series usually arise as the Taylor series of some known function.
  • In many situations [latex]c[/latex] is equal to zero—for instance, when considering a Maclaurin series. In such cases, the power series takes the simpler form [latex]f(x) = \sum_{n=0}^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots[/latex].
  • A power series will converge for some values of the variable [latex]x[/latex] and may diverge for others. If there exists a number [latex]r[/latex] with [latex]0 < r \leq \infty[/latex] such that the series converges when [latex]\left| x-c \right| <r[/latex] and diverges when [latex]\left| x-c \right| >r[/latex], the number [latex]r[/latex] is called the radius of convergence of the power series.

Key Terms

  • Z-transform: transform that converts a discrete time-domain signal into a complex frequency-domain representation
  • combinatorics: a branch of mathematics that studies (usually finite) collections of objects that satisfy specified criteria and their structures
A power series (in one variable) is an infinite series of the form: [latex-display]\displaystyle{f(x) = \sum_{n=0}^\infty a_n \left( x-c \right)^n = a_0 + a_1 (x-c)^1 + a_2 (x-c)^2 + \cdots}[/latex-display] where [latex]a_n[/latex] represents the coefficient of the [latex]n[/latex]th term, [latex]c[/latex] is a constant, and [latex]x[/latex] varies around [latex]c[/latex] (for this reason one sometimes speaks of the series as being centered at [latex]c[/latex]). This series usually arises as the Taylor series of some known function. Any polynomial can be easily expressed as a power series around any center [latex]c[/latex], albeit one with most coefficients equal to zero. For instance, the polynomial [latex-display]f(x) = x^2 + 2x + 3[/latex-display] can be written as a power series around the center [latex]c=1[/latex] as: [latex-display]f(x) = 6 + 4 (x-1) + 1(x-1)^2 + 0(x-1)^3 + 0(x-1)^4 + \cdots \,[/latex-display] or, indeed, around any other center [latex]c[/latex].
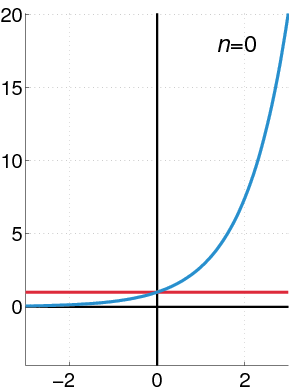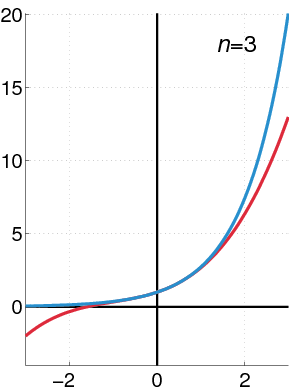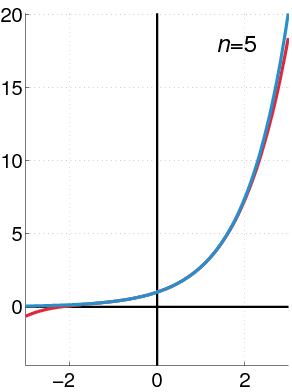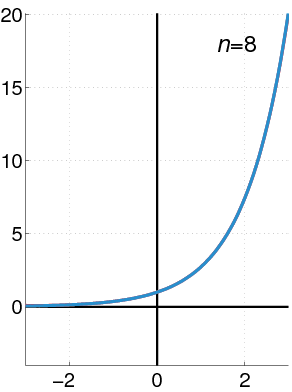
image

Exponential Function as a Power Series: The exponential function (in blue), and the sum of the first [latex]n+1[/latex] terms of its Maclaurin power series (in red).

In many situations [latex]c[/latex] is equal to zero—for instance, when considering a Maclaurin series. In such cases, the power series takes the simpler form [latex-display]\displaystyle{f(x) = \sum_{n=0}^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots}[/latex-display] These power series arise primarily in real and complex analysis, but also occur in combinatorics (under the name of generating functions) and in electrical engineering (under the name of the [latex]Z[/latex]-transform). The familiar decimal notation for real numbers can also be viewed as an example of a power series, with integer coefficients, but with the argument [latex]x[/latex] fixed at [latex]\frac{1}{10}[/latex]. In number theory, the concept of [latex]p[/latex]-adic numbers is also closely related to that of a power series.

Radius of Convergence

A power series will converge for some values of the variable [latex]x[/latex] and may diverge for others. All power series [latex]f(x)[/latex] in powers of [latex](x-c)[/latex] will converge at [latex]x=c[/latex]. If [latex]c[/latex] is not the only convergent point, then there is always a number [latex]r[/latex] with 0 < r ≤ ∞ such that the series converges whenever [latex]\left| x-c \right| <r[/latex] and diverges whenever [latex]\left| x-c \right| >r[/latex]. The number [latex]r[/latex] is called the radius of convergence of the power series. According to the Cauchy-Hadamard theorem, the radius [latex]r[/latex] can be computed from [latex-display]\displaystyle{r^{-1}=\lim_{n\to\infty}\left|{a_{n+1}\over a_n}\right|}[/latex-display] if this limit exists.

Expressing Functions as Power Functions

A power function is a function of the form [latex]f(x) = cx^r[/latex] where [latex]c[/latex] and [latex]r[/latex] are constant real numbers.

Learning Objectives

Describe the relationship between the power functions and infinitely differentiable functions

Key Takeaways

Key Points

  • Since all infinitely differentiable functions can be represented in power series, any infinitely differentiable function can be represented as a sum of many power functions (of integer exponents ).
  • Therefore, an arbitrary function that is infinitely differentiable is expressed as an infinite sum of power functions ([latex]x^n[/latex]) of integer exponent: [latex]f(x) = \sum_{n=0} ^ {\infty} \frac {f^{(n)}(0)}{n! } \, x^{n}[/latex].
  • Functions of the form [latex]f(x) = x^{3}[/latex], [latex]f(x) = x^{1.2}[/latex], [latex]f(x) = x^{-4}[/latex] are all power functions.

Key Terms

  • differentiable: having a derivative, said of a function whose domain and co-domain are manifolds
  • power law: any of many mathematical relationships in which something is related to something else by an equation of the form [latex]f(x) = a x^k[/latex]
A power function is a function of the form [latex]f(x) = cx^r[/latex] where [latex]c[/latex] and [latex]r[/latex] are constant real numbers. Polynomials are made of power functions. Since all infinitely differentiable functions can be represented in power series, any infinitely differentiable function can be represented as a sum of many power functions (of integer exponents). The domain of a power function can sometimes be all real numbers, but generally a non-negative value is used to avoid problems with simplifying. The domain of definition is determined by each individual case. Power functions are a special case of power law relationships, which appear throughout mathematics and statistics. The Taylor series of a real or complex-valued function [latex]f(x)[/latex] that is infinitely differentiable in a neighborhood of a real or complex number [latex]a[/latex] is the power series: [latex-display]\displaystyle{\sum_{n=0} ^ {\infty} \frac {f^{(n)}(a)}{n! } \, (x-a)^{n}}[/latex-display] where [latex]n![/latex] denotes the factorial of [latex]n[/latex] and [latex]f^na[/latex] denotes the [latex]n[/latex]th derivative of [latex]f[/latex] evaluated at the point [latex]x=a[/latex]. Any finite number of initial terms of the Taylor series of a function is called a Taylor polynomial. If the Taylor series is centered at zero, then that series is also called a Maclaurin series: [latex-display]\displaystyle{f(x) = \sum_{n=0} ^ {\infty} \frac {f^{(n)}(0)}{n! } \, x^{n}}[/latex-display] Therefore, an arbitrary function that is infinitely differentiable is expressed as an infinite sum of power functions ([latex]x^n[/latex]) of integer exponent.
image

[latex]\sin x[/latex] in Taylor Approximations: Figure shows [latex]\sin x[/latex] and Taylor approximations, polynomials of degree 1, 3, 5, 7, 9, 11 and 13. As more power functions with larger exponents are added, the Taylor polynomial approaches the correct function.

Examples

Functions of the form [latex]f(x) = x^3[/latex], [latex]f(x) = x^{1.2}[/latex], [latex]f(x) = x^{-4}[/latex] are all power functions.

Taylor and Maclaurin Series

Taylor series represents a function as an infinite sum of terms calculated from the values of the function's derivatives at a single point.

Learning Objectives

Identify a Maclaurin series as a special case of a Taylor series

Key Takeaways

Key Points

  • Any finite number of initial terms of the Taylor series of a function is called a Taylor polynomial.
  • A function that is equal to its Taylor series in an open interval (or a disc in the complex plane) is known as an analytic function.
  • The Taylor series of a real or complex-valued function [latex]f(x)[/latex] that is infinitely differentiable in a neighborhood of a real or complex number a is the power series [latex]f(x)=∑∞n=0f(n)(a)n!(x−a)nf(x) = \sum_{n=0} ^ {\infty} \frac {f^{(n)}(a)}{n! } \, (x-a)^{n}[/latex]. If [latex]a = 0[/latex], the series is called a Maclaurin series.

Key Terms

  • differentiable: having a derivative, said of a function whose domain and co-domain are manifolds
  • analytic function: a real valued function which is uniquely defined through its derivatives at one point
A Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point. The concept of a Taylor series was formally introduced by the English mathematician Brook Taylor in 1715. If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. It is common practice to approximate a function by using a finite number of terms of its Taylor series. Taylor's theorem gives quantitative estimates on the error in this approximation. Any finite number of initial terms of the Taylor series of a function is called a Taylor polynomial. The Taylor series of a function is the limit of that function's Taylor polynomials, provided that the limit exists. A function may not be equal to its Taylor series, even if its Taylor series converges at every point. A function that is equal to its Taylor series in an open interval (or a disc in the complex plane) is known as an analytic function.
image

Exponential Function as a Power Series: The exponential function (in blue) and the sum of the first [latex]n+1[/latex] terms of its Taylor series at [latex]0[/latex] (in red) up to [latex]n=8[/latex].

The Taylor series of a real or complex-valued function [latex]f(x)[/latex] that is infinitely differentiable in a neighborhood of a real or complex number [latex]a[/latex] is the power series: [latex-display]\begin{align} f(x) &= f(a)+\frac {f'(a)}{1! } (x-a)+ \frac{f''(a)}{2! } (x-a)^2+ \cdots \\ &= \sum_{n=0} ^ {\infty} \frac {f^{(n)}(a)}{n! } \, (x-a)^{n} \end{align}[/latex-display] where [latex]n![/latex] denotes the factorial of [latex]n[/latex] and [latex]f^na[/latex] denotes the [latex]n[/latex]th derivative of [latex]f[/latex] evaluated at the point [latex]x=a[/latex]. The derivative of order zero [latex]f[/latex] is defined to be [latex]f[/latex] itself, and [latex](x − a)^0[/latex] and [latex]0![/latex] are both defined to be [latex]1[/latex]. In the case that [latex]a=0[/latex], the series is also called a Maclaurin series.

Example 1

The Maclaurin series for [latex](1 − x)^{−1}[/latex] for [latex]\left| x \right| < 1[/latex] is the geometric series: [latex]1+x+x^2+x^3+\cdots\![/latex] so the Taylor series for [latex]x^{−1}[/latex] at [latex]a=1[/latex] is: [latex-display]1-(x-1)+(x-1)^2-(x-1)^3+\cdots[/latex-display]

Example 2

The Taylor series for the exponential function [latex]e^x[/latex] at [latex]a=0[/latex] is: [latex-display]\displaystyle{1 + \frac{x^1}{1! } + \frac{x^2}{2! } + \frac{x^3}{3! } + \frac{x^4}{4! } + \frac{x^5}{5! }+ \cdots \\= 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} + \cdots\! \\= \sum_{n=0}^\infty \frac{x^n}{n! }}[/latex-display]

Applications of Taylor Series

Taylor series expansion can help approximating values of functions and evaluating definite integrals.

Learning Objectives

Describe applications of the Taylor series expansion

Key Takeaways

Key Points

  • The partial sums of the series, which is called the Taylor polynomials, can be used as approximations of the entire function.
  • Differentiation and integration of power series can be performed term by term, and hence could be easier than directly working with the original function.
  • The (truncated) series can be used to compute function values numerically. This is particularly useful in evaluating special mathematical functions (such as Bessel function).

Key Terms

  • definite integral: the integral of a function between an upper and lower limit
  • complex analysis: theory of functions of a complex variable; a branch of mathematical analysis that investigates functions of complex numbers
  • analytic function: a real valued function which is uniquely defined through its derivatives at one point
Uses of the Taylor series for analytic functions include: 1. The partial sums (the Taylor polynomials) of the series can be used as approximations of the entire function. These approximations are often good enough if sufficiently many terms are included. Approximations using the first few terms of a Taylor series can make otherwise unsolvable problems possible for a restricted domain; this approach is often used in physics.
image

Taylor Polynomials: As more terms are added to the Taylor polynomial, it approaches the correct function. This image shows [latex]\sin x[/latex] and its Taylor approximations, polynomials of degree 1, 3, 5, 7, 9, 11 and 13.

2. Differentiation and integration of power series can be performed term by term and is hence particularly easy. Taylor series is especially useful in evaluating definite integrals. For example, to evaluate [latex]\int_{0}^{1} e^{x^3} \, dx[/latex], the Taylor series expansion of [latex]e^t= \sum_{n=0}^{\infty} \frac{1}{n! } \, t^n[/latex]and the substitution of [latex]t=x^3[/latex] can be used. Since each term in the summation can be integrated separately, we can evaluate the definite integral as long as the sum converges. 3. An analytic function is uniquely extended to a holomorphic function on an open disk in the complex plane. This makes the machinery of complex analysis available. 4. The (truncated) series can be used to compute function values numerically. This is particularly useful in evaluating special mathematical functions (such as Bessel function). 5. Algebraic operations can be done readily on the power series representation; for instance the Euler's formula follows from Taylor series expansions for trigonometric and exponential functions. [latex]e^{ix}[/latex] can be found from the Taylor expansion of [latex]\cos(x)[/latex] and [latex]\sin(x)[/latex]: [latex-display]\displaystyle{\cos(x) = 1-\frac{x^2}{2!}+\frac{x^4}{4! } -\frac{x^6}{6! }+ \cdots}[/latex-display] [latex-display]\displaystyle{\sin(x) = x - \frac{x^3}{3!}+\frac{x^5}{5! } -\frac{x^7}{7! } + \cdots}[/latex-display] and adding the two terms together yields: [latex-display]\begin{align} cos(x)+i\,sin(x) & = (1-\frac{x^2}{2!}+\frac{x^4}{4! } - \cdots) + i (x - \frac{x^3}{3! } + \frac{x^5}{5! } - \cdots) \\ & = 1 + ix + \frac{(ix)^2}{2! } + \frac{(ix)^3}{3! }+ \frac{(ix)^4}{4! } + \cdots \\ & = e^{ix} \end{align}[/latex-display] This result is of fundamental importance in many fields of mathematics (for example, in complex analysis), physics and engineering.

Summing an Infinite Series

Infinite sequences and series can either converge or diverge.

Learning Objectives

Describe properties of the infinite series

Key Takeaways

Key Points

  • Infinite sequences and series continue indefinitely.
  • A series is said to converge when the sequence of partial sums has a finite limit.
  • A series is said to diverge when the limit is infinite or does not exist.

Key Terms

  • limit: a value to which a sequence or function converges
  • sequence: an ordered list of objects
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely. Unlike finite summations, infinite series need tools from mathematical analysis, and specifically the notion of limits, to be fully understood and manipulated. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, and finance. For any infinite sequence of real or complex numbers, the associated series is defined as the ordered formal sum [latex-display]\displaystyle{\sum_{n=0}^{\infty}a_n = a_0 + a_1 + a_2 + \cdots}[/latex-display] The sequence of partial sums [latex]{S_k}[/latex] associated to a series [latex]\sum_{n=0}^\infty a_n[/latex] is defined for each k as the sum of the sequence [latex]{a_n}[/latex] from [latex]a_0[/latex] to [latex]a_k[/latex]: [latex-display]\displaystyle{S_k = \sum_{n=0}^{k}a_n = a_0 + a_1 + \cdots + a_k}[/latex-display] Infinite sequences and series can either converge or diverge. A series is said to converge when the sequence of partial sums has a finite limit. By definition the series [latex]\sum_{n=0}^\infty a_n[/latex] converges to a limit [latex]L[/latex] if and only if the associated sequence of partial sums  converges to [latex]L[/latex]. This definition is usually written as: [latex-display]\displaystyle{L = \sum_{n=0}^{\infty}a_n \Leftrightarrow L = \lim_{k \rightarrow \infty} S_k}[/latex-display] If the limit of is infinite or does not exist, the series is said to diverge.
image

Infinite Series: An infinite sequence of real numbers shown in blue dots. This sequence is neither increasing, nor decreasing, nor convergent, nor Cauchy. It is, however, bounded.

An easy way that an infinite series can converge is if all the [latex]a_{n}[/latex] are zero for sufficiently large [latex]n[/latex]s. Such a series can be identified with a finite sum, so it is only infinite in a trivial sense. Working out the properties of the series that converge even if infinitely many terms are non-zero is, therefore, the essence of the study of series. In the following atoms, we will study how to tell whether a series converges or not and how to compute the sum of a series when such a value exists.

Convergence of Series with Positive Terms

For a sequence [latex]\{a_n\}[/latex], where [latex]a_n[/latex] is a non-negative real number for every [latex]n[/latex], the sum [latex]\sum_{n=0}^{\infty}a_n[/latex] can either converge or diverge to [latex]\infty[/latex].

Learning Objectives

Identify convergence conditions for a sequence with positive terms

Key Takeaways

Key Points

  • Because the partial sum [latex]S_k[/latex] of a series with non-negative terms can only increase as [latex]k[/latex] becomes larger, the limit of the partial sum can either converge or diverge to [latex]\infty[/latex].
  • A geometric sum [latex]1 + \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+\cdots+ \frac{1}{2^n}+\cdots[/latex] converges to [latex]2[/latex], which can be understood visually.
  • The series [latex]\sum_{n \ge 1} \frac{1}{n^2}[/latex] is convergent. This can be seen by comparing individual terms of the series with a sequence [latex]\left( b_n = \frac{1}{n-1} - \frac{1}{n} \right)[/latex], which is know to converge.

Key Terms

  • converge: of a sequence, to have a limit
  • convergence test: methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence, or divergence of an infinite series
For a sequence [latex]\{a_n\}[/latex], where [latex]a_n[/latex] is a non-negative real number for every [latex]n[/latex], the sequence of partial sums [latex-display]S_k = \sum_{n=0}^{k}a_n = a_0 + a_1 + \cdots + a_k[/latex-display] is non-decreasing. Because the partial sum [latex]S_k[/latex] can only increase as [latex]k[/latex] becomes larger, the limit of the partial sum can either converge or diverge to [latex]\infty[/latex]. Therefore, it follows that a series [latex]\sum_{n=0}^{\infty} a_n[/latex] with non-negative terms converges if and only if the sequence [latex]S_k[/latex] of partial sums is bounded.

Example 1

The series [latex]\sum_{n \ge 1} \frac{1}{n^2}[/latex] is convergent because of the inequality: [latex-display]\displaystyle{\frac1 {n^2} \le \frac{1}{n-1} - \frac{1}{n}, (n \ge 2)}[/latex-display] and because: [latex-display]\displaystyle{\sum_{n \ge 2} \left(\frac{1}{n-1} - \frac{1}{n} \right) =\left(1-\frac{1}{2}\right) + \left(\frac{1}{2}-\frac{1}{3}\right) + \left(\frac{1}{3}-\frac{1}{4}\right) + \cdots = 1}[/latex-display]

Example 2

Would the series [latex-display]\displaystyle{S = 1 + \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+\cdots+ \frac{1}{2^n}+\cdots}[/latex-display] converge? It is possible to "visualize" its convergence on the real number line? We can imagine a line of length [latex]2[/latex], with successive segments marked off of lengths [latex]1[/latex], [latex]\frac{1}{2}[/latex], [latex]\frac{1}{4}[/latex], etc. There is always room to mark the next segment, because the amount of line remaining is always the same as the last segment marked: when we have marked off [latex]\frac{1}{2}[/latex], we still have a piece of length [latex]\frac{1}{2}[/latex] unmarked, so we can certainly mark the next [latex]\frac{1}{4}[/latex]. This argument does not prove that the sum is equal to [latex]2[/latex] (although it is), but it does prove that it is at most [latex]2[/latex]. In other words, the series has an upper bound. Proving that the series is equal to [latex]2[/latex] requires only elementary algebra, however. If the series is denoted [latex]S[/latex], it can be seen that: [latex-display]\displaystyle{\frac{S}{2} \,= \frac{1+ \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+\cdots}{2} \\ \quad= \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \frac{1}{16} +\cdots}[/latex-display] Therefore: [latex-display]\displaystyle{S-\frac{S}{2} = 1\\S = 2}[/latex-display]
image

Geometric Sum: Visualization of the geometric sum in Example 2. The length of the line ([latex]2[/latex]) can contain all the successive segments marked off of lengths [latex]1[/latex], [latex]\frac{1}{2}[/latex], [latex]\frac{1}{4}[/latex], etc.

For these specific examples, there are easy ways to check the convergence. However, it could be the case that there are no easy ways to check the convergence. For these general cases, we can experiment with several well-known convergence tests (such as ratio test, integral test, etc.). We will learn some of these tests in the following atoms.

Licenses & Attributions

CC licensed content, Shared previously

CC licensed content, Specific attribution