We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts

J1.03: Section 1 Part 2

Example 1: Fitting an exponential model to find the growth rate

Use this data from the first 10 U.S. censuses to make an exponential model of U.S. population growth, then use that model to answer these questions: [Use the Exponential Model worksheet in Models.xls.]
  1. Does an exponential model fit this data well? How do you know?
  2. What was the average annual growth rate during this period?
  3. What population does the model predict for 1900? For 2000?

Solution procedure:

[1] Redefine the input variable to “Years since 1780”, adjusting the x values in column A to start at 0.
Year Population (millions)
1780 2.8
1790 3.9
1800 5.3
1810 7.2
1820 9.6
1830 12.9
1840 17.1
1850 23.2
1860 31.4
1870 39.8
[2] Copy the redefined data values into a copy of the Exponential Model template. The numbers should fill rows 3 to 12 in columns A and B. [3] Select cells C3, D3, and E3. Then spread them (and the formulas they already contain) down to row 12. All three columns should now show numbers. [The formula in C3 is “=$G$3*(1+$G$4)^A3”.][2] Copy the redefined data values into a copy of the Exponential Model template. The numbers should fill rows 3 to 12 in columns A and B. [4] Make a scatter plot of columns A, B, & C. This will show the data and the model on the same graph. At first, the model points will be on a horizontal line through the origin, but they will move as the exponential growth-rate model parameters (in G3 and G4) are adjusted. [5] Adjust G3 (initial value) and G4 (growth rate) to make the model approximately match the data.
  1. Set G3 to 2.8, the first value in the table. (We can later adjust this to reduce standard deviation).
  2. Set G4 to 0.01 (which is 1%), then adjust it until the shape of the model is close to that of the data at about 0.03 (which is 3%).
[6] Adjust the parameters using feedback from the graph until further adjustments do not significantly improve the fit. EXPONENTIAL-GROWTH WORKSHEET FROM Models.xls FILLED OUT WITH EXAMPLE 1 DATA
  A B C D E F G H
1 x y data y model Data-Model Exponential model: y = a * (1+r)^x
2 Year-1780 Height Prediction deviation y = 2.8 * (1+0.03)^x
3   0 2.8 2.80 0.0000 2.8 a: Initial value at x=0
4 10 3.9 3.76 0.1370
0.03 r: Growth rate
5 20 5.3 5.06 0.2429  
6 30 7.2 6.80 0.4037  
7 40 9.6 9.13 0.4663 Model and data value counts
8 50 12.9 12.27 0.6251 2 Number of parameters
9 60 17.1 16.50 0.6035 10 Number of data points
10 70 23.2 22.17 1.0301  
11 80 31.4 29.79 1.6055 Goodness of fit of this model
12 90 39.8 40.04 -0.2413 4.910062 Sum of squared deviat
13 120 97.19 0.783427 Standard deviation
14 220 1867.87  
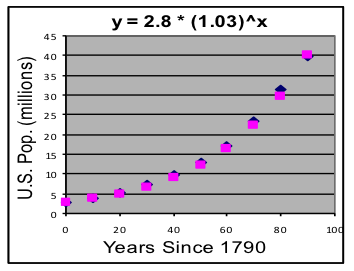graph1 Answers to questions asked: [a] Yes, this model fits the data well, since the deviations are only a few percent of the typical population values. [b] The model growth-rate parameter shows the average annual growth rate of U.S. population from 1780 to 1870 was about 3.0%. [c] Evaluate the model at 120 (1900 is 120 years since 1780), and 220 (for 2000) to show that a model based on the 1780-1870 census data predicts a U.S. population of about 97 million in 1900 and 1,868 million in 2000. (Actual population was 76 million in 1900 and 281 million in 2000, showing that the rate of U.S. population growth slowed down substantially after 1870.)

Licenses & Attributions

CC licensed content, Shared previously

  • Mathematics for Modeling. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution.