We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts

H1.06: Example 4

Example 4: Write a mathematical model for the population of this city over the given period of time and use that to predict the population in 2010.
Year 1970 1980 1990 2000
Pop’n (thousands) 234 289.5 345 400.5
Solution: 1. What are the two variables? And what are their units?  Ans. Year and population. Year is in years and population is in thousands of people. 2. What will we predict? (Make it y.) What are some points? Ans. We will predict population. So y = population. Year is the input variable. However, as we saw Example 3, it will be more convenient to have the input variable x = years since 1970.   Then x is greater than or equal to zero. Obviously y must also be greater than or equal to zero. 1970 has pop’n of 234. So x = 0 and y = 234. Use the point (0, 234) 1980 has pop’n of 289.5.   So x = 10 and y = 289.5. Use the point (10,289.5)  3. Is a linear model appropriate?
year year - 1970 popn
1970 0 234
1980 10 289.5
1990 20 345
2000 30 400.5
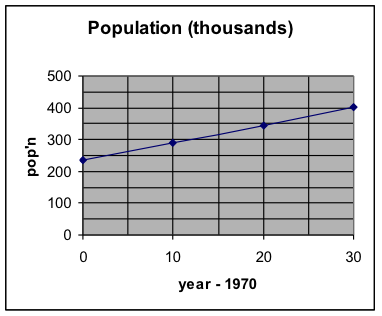graph6 The graph clearly indicates that a linear model is appropriate for this population growth over this time period. 4. Slope: Find the slope: m = rise / run Let (0,234) be the first point and (10,289.5) be the second point.

[latex]m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{289.5-234}{10-0}=\frac{55.5}{10}=5.55[/latex]

Interpret the slope, using the units of the numbers in the problem: (As x increases by 1, y increases by m.) For each year that goes by, population will increase by 5.55 thousand people. 5. Write the formula for the linear relationship: (Choose either point and use the point-slope form of the line. Then simplify it to the slope-intercept form of the line.) Choose (0,234) for the point and use the slope of 5.55 that I just computed.

[latex]\begin{align}&y-{{y}_{0}}=m(x-{{x}_{0}})\\&y-234=5.55(x-0)\\&y-234=5.55x\\&y=5.55x+234\\\end{align}[/latex]

6. Interpret the y-intercept. (The value of y is b when [latex]x=0[/latex].) When [latex]x=0[/latex], that is, in 1970, the population is 234 thousand people. 7. Use the formula to make the requested prediction.   Write the result in a sentence, with units. For 2010, [latex]x=2010-1970=40[/latex].

[latex]\begin{align}&y=5.55x+234\\&y=5.55(40)+234\\&y=222+234\\&y=456\\\end{align}[/latex]

So, in 2010, the model predicts that the population will be 456 thousand people. 8. Sketch a graph from the original problem information, use it to estimate the answers to the prediction questions, and determine whether your answers from the algebraic formula are reasonable. We take the same graph as before and extend it to the right so that we can estimate a population value for x = 40.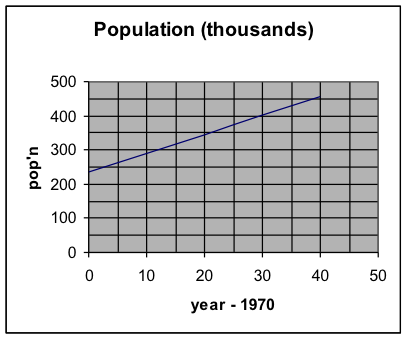 graph7 The value we see from the graph is approximately 450 thousand people. That is consistent with the value we obtained from the formula. The prediction is reasonable.

Licenses & Attributions

CC licensed content, Shared previously

  • Mathematics for Modeling. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution.